Simple Harmonic Motion 3 Question 11
11. A thin rod of length
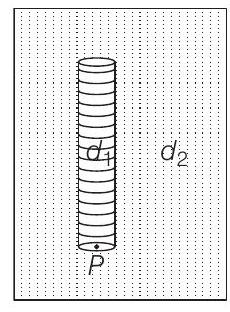
The density
Show Answer
Answer:
Correct Answer: 11.
Solution:
- Let
Given that,
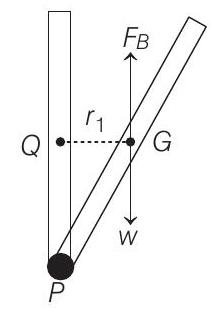
Here, negative sign shows the restoring nature of torque.
From Eq. (i), we see that
Hence, motion of the rod will be simple harmonic.
Rewriting Eq. (i) as
Here,
Substituting this value of
Comparing this equation with standard differential equation of SHM, i.e.
The angular frequency of oscillation is






