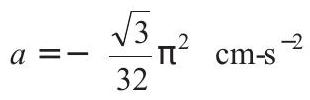SATHEE: Simple Harmonic Motion 2 Question 2

Simple Harmonic Motion 2 Question 2

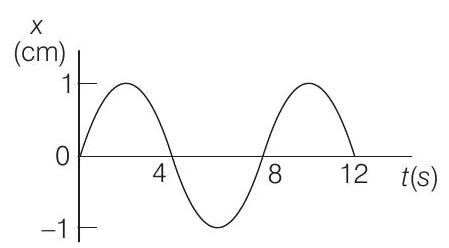
2. The $x$ - $t$ graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at $t = 4 / 3 s$ is

(a) $\frac{\sqrt{3}}{32} π^{2} c m s^{- 2}$

(b) $\frac{- π^{2}}{32} c m s^{- 2}$

(d) $- \frac{\sqrt{3}}{32} π^{2} c m s^{- 2}$

Show Answer

Answer:

Correct Answer: 2. (d)

Solution:

$T = 8 s, ω = \frac{2 π}{T} = \frac{π}{4} {rads}^{- 1}$

$\begin{aligned} \Rightarrow x = A \sin ω t \\ ∴ a = - ω^{2} x = - \frac{π^{2}}{16} \sin \frac{π}{4} t \end{aligned}$

Substituting $t = \frac{4}{3} s$ , we get

Play Store

App Store

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".

Simple Harmonic Motion 2 Question 2

2. The x - t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t=4/3s is

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

2. The $x$ - $t$ graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at $t = 4 / 3 s$ is