Rotation 5 Question 6
15. A block of base $10 cm \times 10 cm$ and height $15 cm$ is kept on an inclined plane. The coefficient of friction between them is $\sqrt{3}$. The inclination $\theta$ of this inclined plane from the horizontal plane is gradually increased from $0^{\circ}$. Then,
(2009)
(a) at $\theta=30^{\circ}$, the block will start sliding down the plane
(b) the block will remain at rest on the plane up to $\operatorname{certain} \theta$ and then it will topple
(c) at $\theta=60^{\circ}$, the block will start sliding down the plane and continue to do so at higher angles
(d) at $\theta=60^{\circ}$, the block will start sliding down the plane and on further increasing $\theta$, it will topple at $\operatorname{certain} \theta$
Show Answer
Answer:
Correct Answer: 15. (b)
Solution:
- Condition of sliding is
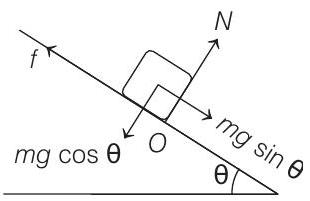
$m g \sin \theta>\mu m g \cos \theta$
or $\tan \theta>\mu$ or $\tan \theta>\sqrt{3}$
Condition of toppling is
Torque of $m g \sin \theta$ about $0>$ torque of $m g \cos \theta$ about
$$ \begin{array}{ll} \therefore & (m g \sin \theta) \frac{15}{2}>(m g \cos \theta) \frac{10}{2} \\ \text { or } & \tan \theta>\frac{2}{3} \end{array} $$
With increase in value of $\theta$, condition of sliding is satisfied first.
16. $\mathbf{L}=m(\mathbf{r} \times \mathbf{v})$
Direction of $(\mathbf{r} \times \mathbf{v})$, hence the direction of angular momentum remains the same.






