SATHEE: Rotation 5 Question 6

Rotation 5 Question 6

15. A block of base $10 c m \times 10 c m$ and height $15 c m$ is kept on an inclined plane. The coefficient of friction between them is $\sqrt{3}$ . The inclination $θ$ of this inclined plane from the horizontal plane is gradually increased from $0^{\circ}$ . Then,

(2009)

(a) at $θ = 30^{\circ}$ , the block will start sliding down the plane

(b) the block will remain at rest on the plane up to $certain θ$ and then it will topple

(d) at $θ = 60^{\circ}$ , the block will start sliding down the plane and on further increasing $θ$ , it will topple at $certain θ$

Show Answer

Answer:

Correct Answer: 15. (b)

Solution:

Condition of sliding is

$m g \sin θ > μ m g \cos θ$

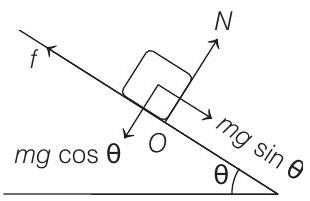
or $\tan θ > μ$ or $\tan θ > \sqrt{3}$

Condition of toppling is

Torque of $m g \sin θ$ about $0 >$ torque of $m g \cos θ$ about

$\begin{array}{ll} ∴ & (m g \sin θ) \frac{15}{2} > (m g \cos θ) \frac{10}{2} \\ or & \tan θ > \frac{2}{3} \end{array}$

With increase in value of $θ$ , condition of sliding is satisfied first.

16. $L = m (r \times v)$

Direction of $(r \times v)$ , hence the direction of angular momentum remains the same.

पिछला

अगला

Rotation 5 Question 6

15. A block of base $10 c m \times 10 c m$ and height $15 c m$ is kept on an inclined plane. The coefficient of friction between them is $\sqrt{3}$ . The inclination $θ$ of this inclined plane from the horizontal plane is gradually increased from $0^{\circ}$ . Then,

Answer:

16. $L = m (r \times v)$

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Rotation 5 Question 6

15. A block of base 10cm×10cm and height 15cm is kept on an inclined plane. The coefficient of friction between them is 3. The inclination θ of this inclined plane from the horizontal plane is gradually increased from 0∘. Then,

Answer:

16. L=m(r×v)

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

15. A block of base $10 c m \times 10 c m$ and height $15 c m$ is kept on an inclined plane. The coefficient of friction between them is $\sqrt{3}$ . The inclination $θ$ of this inclined plane from the horizontal plane is gradually increased from $0^{\circ}$ . Then,

16. $L = m (r \times v)$