Rotation 5 Question 26
38. A uniform circular disc has radius $R$ and mass $m$. A particle, also of mass $m$, is fixed at a point $A$ on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord $P Q$ that is
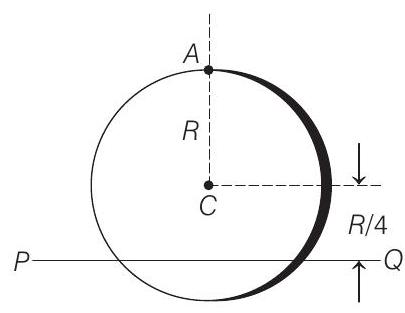at a distance $R / 4$ from the centre $C$ of the disc. The line $A C$ is perpendicular to $P Q$. Initially the disc is held vertical with the point $A$ at its highest position. It is then allowed to fall, so that it starts rotation about $P Q$. Find the linear speed of the particle as it reaches its lowest position.
(1998, 8M)
Show Answer
Answer:
Correct Answer: 38. $\sqrt{5 g R}$
Solution:
- Initial and final positions are shown below.
Decrease in potential energy of mass
$$ =m g \quad 2 \times \frac{5 R}{4}=\frac{5 m g R}{2} $$
Decrease in potential energy of disc $=m g \quad 2 \times \frac{R}{4}=\frac{m g R}{2}$
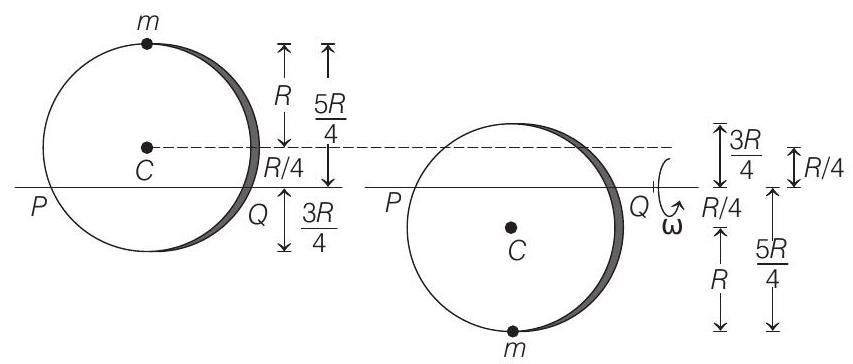
Therefore, total decrease in potential energy of system
$$ =\frac{5 m g R}{2}+\frac{m g R}{2}=3 m g R $$
Gain in kinetic energy of system $=\frac{1}{2} I \omega^{2}$
where, $I=$ moment of inertia of system (disc + mass) about
axis $P Q$
$=$ moment of inertia of disc
- moment of inertia of mass
$=\frac{m R^{2}}{4}+m \frac{R}{4}^{2}+m \frac{5 R}{4}^{2}$
$I=\frac{15 m R^{2}}{8}$
From conservation of mechanical energy,
Decrease in potential energy $=$ Gain in kinetic energy
$$ \begin{aligned} \therefore & & 3 m g R & =\frac{1}{2} \frac{15 m R^{2}}{8} \omega^{2} \\ \Rightarrow & & \omega & =\sqrt{\frac{16 g}{5 R}} \end{aligned} $$
Therefore, linear speed of particle at its lowest point
$$ \begin{aligned} & v=\frac{5 R}{4} \quad \omega=\frac{5 R}{4} \sqrt{\frac{16 g}{5 R}} \\ & v=\sqrt{5 g R} \end{aligned} $$
