SATHEE: Rotation 5 Question 26

Rotation 5 Question 26

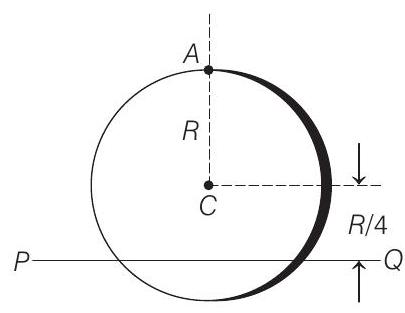38. A uniform circular disc has radius $R$ and mass $m$ . A particle, also of mass $m$ , is fixed at a point $A$ on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord $P Q$ that is

at a distance $R / 4$ from the centre $C$ of the disc. The line $A C$ is perpendicular to $P Q$ . Initially the disc is held vertical with the point $A$ at its highest position. It is then allowed to fall, so that it starts rotation about $P Q$ . Find the linear speed of the particle as it reaches its lowest position.

(1998, 8M)

Show Answer

Answer:

Correct Answer: 38. $\sqrt{5 g R}$

Solution:

Initial and final positions are shown below.

Decrease in potential energy of mass

$= m g 2 \times \frac{5 R}{4} = \frac{5 m g R}{2}$

Decrease in potential energy of disc $= m g 2 \times \frac{R}{4} = \frac{m g R}{2}$

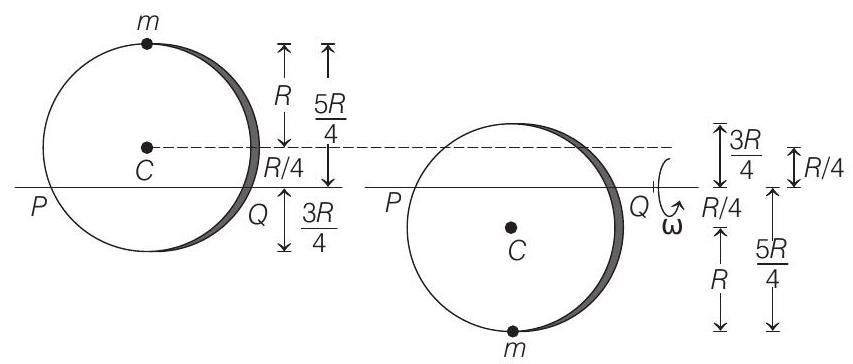
Therefore, total decrease in potential energy of system

$= \frac{5 m g R}{2} + \frac{m g R}{2} = 3 m g R$

Gain in kinetic energy of system $= \frac{1}{2} I ω^{2}$

where, $I =$ moment of inertia of system (disc + mass) about

axis $P Q$

$=$ moment of inertia of disc

moment of inertia of mass

$= \frac{m R^{2}}{4} + m {\frac{R}{4}}^{2} + m {\frac{5 R}{4}}^{2}$

$I = \frac{15 m R^{2}}{8}$

From conservation of mechanical energy,

Decrease in potential energy $=$ Gain in kinetic energy

$\begin{aligned} ∴ & 3 m g R & = \frac{1}{2} \frac{15 m R^{2}}{8} ω^{2} \\ \Rightarrow & ω & = \sqrt{\frac{16 g}{5 R}} \end{aligned}$

Therefore, linear speed of particle at its lowest point

$\begin{aligned} v = \frac{5 R}{4} ω = \frac{5 R}{4} \sqrt{\frac{16 g}{5 R}} \\ v = \sqrt{5 g R} \end{aligned}$

पिछला

अगला

Rotation 5 Question 26

38. A uniform circular disc has radius $R$ and mass $m$ . A particle, also of mass $m$ , is fixed at a point $A$ on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord $P Q$ that is

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Rotation 5 Question 26

38. A uniform circular disc has radius R and mass m. A particle, also of mass m, is fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

38. A uniform circular disc has radius $R$ and mass $m$ . A particle, also of mass $m$ , is fixed at a point $A$ on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord $P Q$ that is