Rotation 4 Question 7
8. Two uniform rods $A$ and $B$ of length $0.6 m$ each and of masses $0.01 kg$ and $0.02 kg$, respectively are rigidly joined end to end. The combination is pivoted at the lighter end, $P$ as shown in figure. Such that it can freely rotate about point $P$ in a vertical plane.
A small object of mass $0.05 kg$, moving horizontally, hits the lower end of the combination and sticks to it. What should be the velocity of the object, so that the system
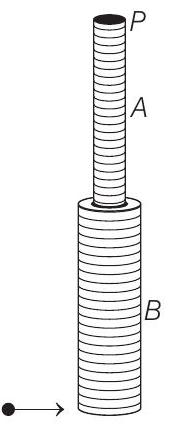 could just be raised to the horizontal position?
could just be raised to the horizontal position?
(1994, 6M)
Show Answer
Answer:
Correct Answer: 8. $6.3 m / s$
Solution:
- System is free to rotate but not free to translate. During collision, net torque on the system ( $\operatorname{rod} A+\operatorname{rod} B+\operatorname{mass} m)$ about point $P$ is zero.
Therefore, angular momentum of system before collision
$=$ angular momentum of system just after collision (about $P$ ).
Let $\omega$ be the angular velocity of system just after collision, then
$$ \Rightarrow \quad m v(2 l)=I \omega $$
$$ L _i=L _f $$
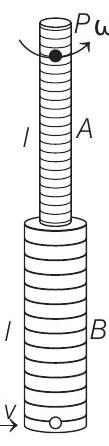
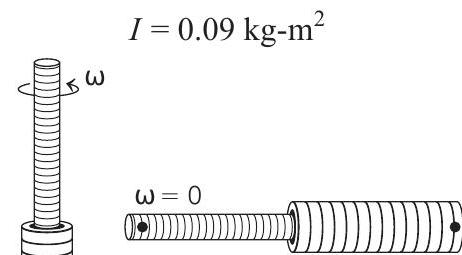
Here, $I=$ moment of inertia of system about $P$
$$ =m(2 l)^{2}+m _A\left(l^{2} / 3\right)+m _B \frac{l^{2}}{12}+\frac{l}{2}+l^{2} $$
Given, $l=0.6 m, m=0.05 kg, m _A$
$$ =0.01 kg \text { and } m _B=0.02 kg \text {. } $$
Substituting the values, we get
Therefore, from Eq. (i)
$$ \begin{aligned} \omega & =\frac{2 m v l}{I}=\frac{(2)(0.05)(v)(0.6)}{0.09} \\ \omega & =0.67 v \end{aligned} $$
Now, after collision, mechanical energy will be conserved. Therefore, decrease in rotational KE
$=$ increase in gravitational $PE$ or $\frac{1}{2} I \omega^{2}=m g(2 l)+m _A g \quad \frac{l}{2}+m _B g\left(l+\frac{l}{2}\right)$
or $\quad \omega^{2}=\frac{g l\left(4 m+m _A+3 m _B\right)}{I}$
$$ \begin{aligned} & =\frac{(9.8)(0.6)(4 \times 0.05+0.01+3 \times 0.02)}{0.09} \\ & =17.64(rad / s)^{2} \end{aligned} $$
$$ \therefore \quad \omega=4.2 rad / s $$
Equating Eqs. (ii) and (iii), we get
$$ v=\frac{4.2}{0.67} m / s \text { or } v=6.3 m / s $$






