Rotation 4 Question 7
8. Two uniform rods
A small object of mass
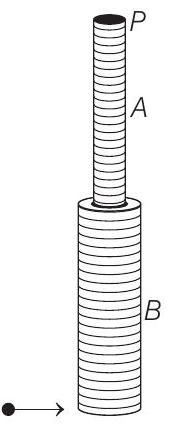 could just be raised to the horizontal position?
could just be raised to the horizontal position?
(1994, 6M)
Show Answer
Answer:
Correct Answer: 8.
Solution:
- System is free to rotate but not free to translate. During collision, net torque on the system (
Therefore, angular momentum of system before collision
Let
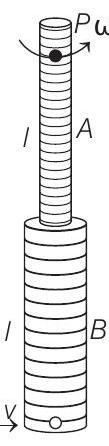
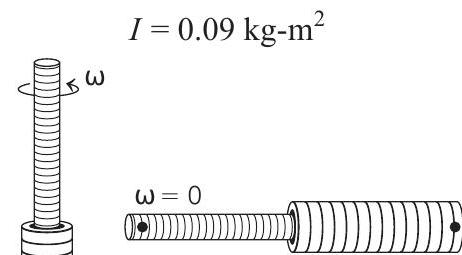
Here,
Given,
Substituting the values, we get
Therefore, from Eq. (i)
Now, after collision, mechanical energy will be conserved. Therefore, decrease in rotational KE
or
Equating Eqs. (ii) and (iii), we get






