Rotation 3 Question 25
31. A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The
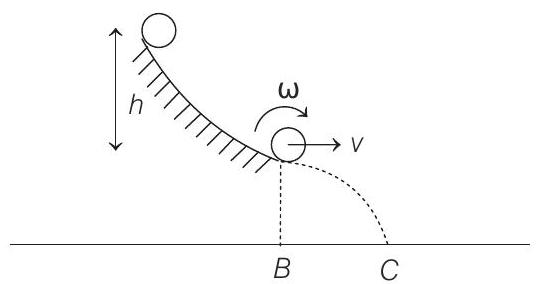
 horizontal part is 1.0 $m$ above the ground level and the top of the track is $2.6 m$ above the ground. Find the distance on the ground with respect to the point $B$ (which is vertically below the end of the track as shown in figure) where the sphere lands. During its flight as a projectile, does the sphere continue to rotate about its centre of mass? Explain.
horizontal part is 1.0 $m$ above the ground level and the top of the track is $2.6 m$ above the ground. Find the distance on the ground with respect to the point $B$ (which is vertically below the end of the track as shown in figure) where the sphere lands. During its flight as a projectile, does the sphere continue to rotate about its centre of mass? Explain.
$(1987,7$ M)
Show Answer
Answer:
Correct Answer: 31. $2.13 m$, yes
Solution:
- $h=2.6-1.0=1.6 m$
During pure rolling mechanical energy remains conserved
So, at bottom of track total kinetic energy of sphere will be $m g h$.
The ratio of $\frac{K _R}{K _T}=\frac{2}{5}$
$$ \begin{array}{rlrl} \text { or } & K _T & =\frac{5}{7} m g h=\frac{1}{2} m v^{2} \\ \therefore & & v & =\sqrt{\frac{10}{7} g h}=\sqrt{\frac{10}{7} \times 9.8 \times 1.6} \\ & & =4.73 m / s \end{array} $$
In projectile motion
Time to fall to ground $=\sqrt{\frac{2 \times 1}{9.8}}=0.45 s$
$\therefore \quad$ The desired distance $B C=v t=2.13 m$
In air, during its flight as a projectile only $m g$ is acting on the sphere which passes through its centre of mass. Therefore, net torque about centre of mass is zero or angular velocity will remain constant.






