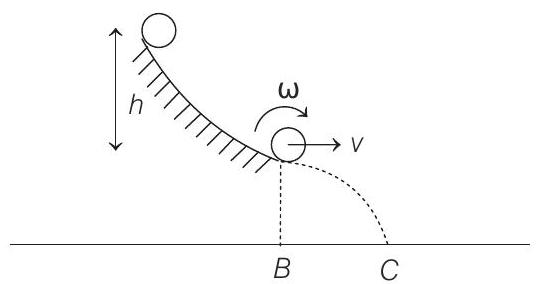
31. A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The
horizontal part is 1.0 above the ground level and the top of the track is above the ground. Find the distance on the ground with respect to the point (which is vertically below the end of the track as shown in figure) where the sphere lands. During its flight as a projectile, does the sphere continue to rotate about its centre of mass? Explain.
M)
Show Answer
Answer:
Correct Answer: 31. , yes
Solution:
During pure rolling mechanical energy remains conserved
So, at bottom of track total kinetic energy of sphere will be .
The ratio of
In projectile motion
Time to fall to ground
The desired distance
In air, during its flight as a projectile only is acting on the sphere which passes through its centre of mass. Therefore, net torque about centre of mass is zero or angular velocity will remain constant.
