Rotation 3 Question 21
27. A boy is pushing a ring of mass $2 kg$ and radius $0.5 m$ with a stick as shown in the figure. The stick applies a force of $2 N$ on the ring and rolls it without slipping with an acceleration of $0.3 m / s^{2}$. The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the
 coefficient of friction between the stick and the ring is $\frac{P}{10}$. The value of $P$ is
coefficient of friction between the stick and the ring is $\frac{P}{10}$. The value of $P$ is
(2011)
Analytical & Descriptive Questions
Show Answer
Answer:
Correct Answer: 27. 3.6
Solution:
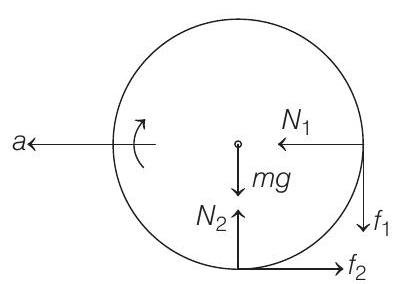
There is no slipping between ring and ground. Hence $f _2$ is not maximum. But there is slipping between ring and stick. Therefore, $f _1$ is maximum. Now let us write the equations.
$$ \begin{gathered} \quad I=m R^{2}=(2)(0.5)^{2} \\ =\frac{1}{2} kg-m^{2} \\ N _1-f _2=m a \\ \text { or } \quad N _1-f _2=(2)(0.3)=0.6 N \\ a=R \alpha=\frac{R \tau}{I}=\frac{R\left(f _2-f _1\right) R}{I}=\frac{R^{2}\left(f _2-f _1\right)}{I} \\ \therefore \quad 0.3=\frac{(0.5)^{2}\left(f _2-f _1\right)}{(1 / 2)} \\ \text { or } \quad f _2-f _1=0.6 N \\ \text { Further } \quad f _1^{2}+f _1^{2}=(2)^{2}=4 \\ f _1=\mu N _1=\frac{P}{10} N _1 \end{gathered} $$
Solving above four equations we get, $P \simeq 3.6$






