Rotation 3 Question 19
24. A cylinder of mass $M$ and radius $R$ is resting on a horizontal platform (which is parallel to the $x-y$ plane) with its axis fixed along the $Y$-axis and free to rotate about its axis. The platform is given a motion in the $x$-direction given by $x=A \cos (\omega t)$. There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is
$(1988,2 M)$
True / False
Show Answer
Answer:
Correct Answer: 24. $\frac{1}{3} M R A \omega^2$ 25. F
Solution:
- Considering the motion of cylinder.
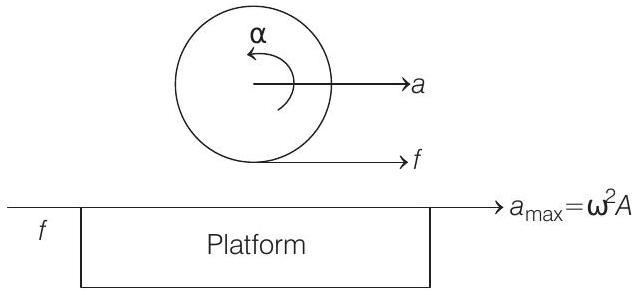
$$ \begin{aligned} a & =\frac{f}{M} \Rightarrow \alpha=\frac{f R}{\frac{M R^{2}}{2}} \\ & =\frac{2 f}{M R} \\ R \alpha & =\frac{2 f}{M} \\ \text { or } \quad \text { Now, } a+R \alpha & =a _{\max }=\omega^{2} A \end{aligned} $$
From Eqs. (i) and (ii), $\quad \frac{v _1}{v _2}=1$ i.e. $v _1=v _2$
or both will reach simultaneously.
NOTE In the question,
$K=$ kinetic energy given to ring and cylinder,
$K _R=$ rotational kinetic energy and
$K _T=$ translational kinetic energy.






