Rotation 3 Question 19
24. A cylinder of mass
True / False
Show Answer
Answer:
Correct Answer: 24.
Solution:
- Considering the motion of cylinder.
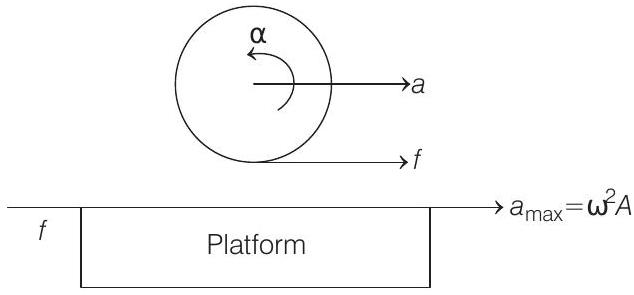
From Eqs. (i) and (ii),
or both will reach simultaneously.
NOTE In the question,






