Rotation 2 Question 4
4. A ring of mass $M$ and radius $R$ is rotating with angular speed $\omega$ about a fixed vertical axis passing through its centre $O$ with two point masses each of mass $\frac{M}{8}$ at rest at $O$. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure.
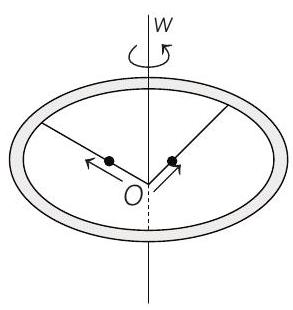At some instant, the angular speed of the system is $\frac{8}{9} \omega$ and one of the masses is at a distance of $\frac{3}{5} R$ from $O$. At this instant, the distance of the other mass from $O$ is
(2015 Adv.)
(a) $\frac{2}{3} R$
(b) $\frac{1}{3} R$
(c) $\frac{3}{5} R$
(d) $\frac{4}{5} R$
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Let the other mass at this instant is at a distance of $x$ from the centre $O$. Applying law of conservation of angular momentum, we have
$$ I _1 \omega _1=I _2 \omega _2 $$
$\therefore$
$\left(M R^{2}\right)(\omega)=M R^{2}+\frac{M}{8} \frac{3}{5} R^{2}+\frac{M}{8} x^{2} \quad \frac{8}{9} \omega$
Solving this equation, we get $x=\frac{4}{5} R$.
NOTE If we take identical situations with both point masses, then answer will be (c). But in that case, angular momentum is not conserved.
