Rotation 2 Question 4
4. A ring of mass
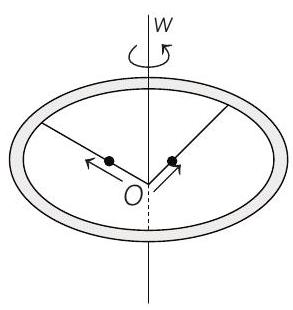 At some instant, the angular speed of the system is
At some instant, the angular speed of the system is
(2015 Adv.)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Let the other mass at this instant is at a distance of
Solving this equation, we get
NOTE If we take identical situations with both point masses, then answer will be (c). But in that case, angular momentum is not conserved.






