Rotation 2 Question 24
24. A particle is projected at time $t=0$ from a point $P$ on the ground with a speed $v _0$, at an angle of $45^{\circ}$ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about $P$ at time $t=\frac{v _0}{g}$.
$(1984,6 M)$
Show Answer
Answer:
Correct Answer: 24. $\frac{m v_0^3}{2 \sqrt{2} g}$ in a direction perpendicular to paper inwards
Solution:
- In terms of $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$
$$ \begin{aligned} & \mathbf{u}=\frac{v _0}{\sqrt{2}} \hat{\mathbf{i}}+\frac{v _0}{\sqrt{2}} \hat{\mathbf{j}} \\ & \Rightarrow \quad \mathbf{a}=-g \hat{\mathbf{j}} \\ & t=\frac{v _0}{g} \\ & =\frac{v _0^{2}}{\sqrt{2} g} \hat{\mathbf{i}}+\frac{v _0^{2}}{\sqrt{2} g} \hat{\mathbf{j}}-\frac{v _0^{2}}{2 g} \hat{\mathbf{j}} \end{aligned} $$
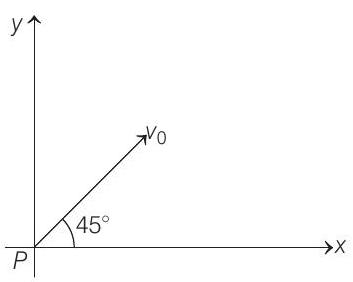
Now, angular momentum about point $P$ at given time
$$ \begin{aligned} \mathbf{L} & =m(\mathbf{r} \times \mathbf{v}) \\ & =m-\frac{v _0^{3}}{\sqrt{2} g}+\frac{v _0^{3}}{2 g}-\frac{v _0^{3}}{2 g}+\frac{v _0^{3}}{2 \sqrt{2} g} \hat{\mathbf{k}} \\ & =-\frac{m v _0^{3}}{2 \sqrt{2} g} \hat{\mathbf{k}} \end{aligned} $$
Thus, magnitude of angular momentum is $\frac{m v _0^{3}}{2 \sqrt{2} g}$ in $-\hat{\mathbf{k}}$ direction i.e. in a direction perpendicular to paper inwards
