Rotation 2 Question 11
11. A disc of mass $M$ and radius $R$ is rolling with angular speed $\omega$ on a horizontal plane as shown. The magnitude of angular momentum of the disc about the origin $O$ is
(1999, 2M)
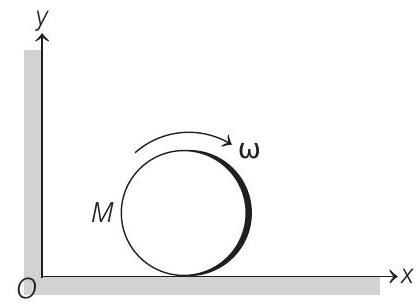
(a) $\frac{1}{2} M R^{2} \omega$
(b) $M R^{2} \omega$
(c) $\frac{3}{2} M R^{2} \omega$
(d) $2 M R^{2} \omega$
Show Answer
Answer:
Correct Answer: 11. (c)
Solution:
- From the theorem
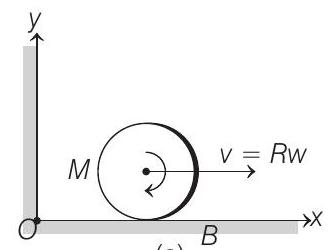
(a)
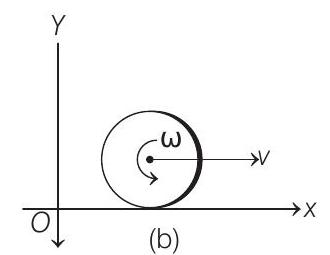
(b)
$$ \mathbf{L} _0=\mathbf{L} _{CM}+M(\mathbf{r} \times \mathbf{v}) $$
We may write
Angular momentum about $O=$ Angular momentum about $CM+$ Angular momentum of $CM$ about origin
$$ \begin{aligned} \therefore \quad L _0 & =I \omega+M R v \\ & =\frac{1}{2} M R^{2} \omega+M R(R \omega)=\frac{3}{2} M R^{2} \omega \end{aligned} $$
NOTE That in this case [ Figure (a) ] both the terms in Eq. (i), i.e. $L _{C M}$ and $M(r \times v)$ have the same direction $\ddot{A}$. That is why, we have used $L _0=/ \omega+M R v$. We will use $L _0=\mid \omega \sim M R v$ if they are in opposite direction as shown in figure (b).






