Rotation 2 Question 11
11. A disc of mass
(1999, 2M)
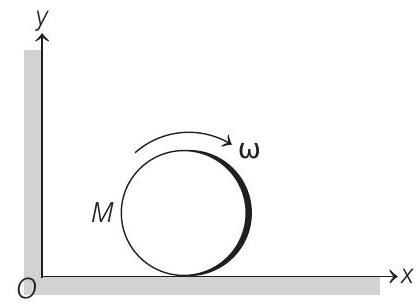
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 11. (c)
Solution:
- From the theorem
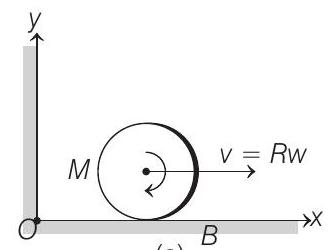
(a)
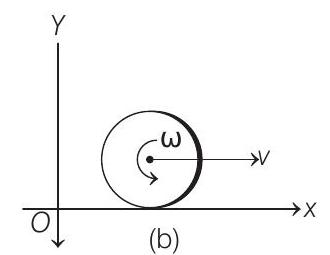
(b)
We may write
Angular momentum about
NOTE That in this case [ Figure (a) ] both the terms in Eq. (i), i.e.






