Rotation 1 Question 3
3. A thin disc of mass $M$ and radius $R$ has mass per unit area $\sigma(r)=k r^{2}$, where $r$ is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is
(2019 Main, 10 April I)
(a) $\frac{M R^{2}}{2}$
(b) $\frac{M R^{2}}{6}$
(c) $\frac{M R^{2}}{3}$
(d) $\frac{2 M R^{2}}{3}$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Given, Surface mass density, $\sigma=k r^{2}$
So, mass of the disc can be calculated by considering small element of area $2 \pi r d r$ on it and then integrating it for complete disc, i.e.
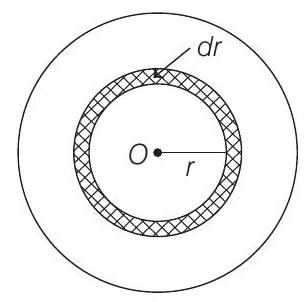
$$ \begin{aligned} d m & =\sigma d A=\sigma \times 2 \pi r d r \\ \int d m & =M=\int _0^{R}\left(k r^{2}\right) 2 \pi r d r \\ \Rightarrow \quad M & =2 \pi k \frac{R^{4}}{4}=\frac{1}{2} \pi k R^{4} \end{aligned} $$
Moment of inertia about the axis of the disc,
$$ \begin{aligned} I & =\int d I=\int d m r^{2}=\int \sigma d A r^{2} \\ & =\int _0^{R} k r^{2}(2 \pi r d r) r^{2} \\ \Rightarrow \quad I & =2 \pi k \int _0^{R} r^{5} d r=\frac{2 \pi k R^{6}}{6}=\frac{\pi k R^{6}}{3} \end{aligned} $$
From Eqs. (i) and (ii), we get
$$ I=\frac{2}{3} M R^{2} $$






