Rotation 1 Question 3
3. A thin disc of mass
(2019 Main, 10 April I)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
- Given, Surface mass density,
So, mass of the disc can be calculated by considering small element of area
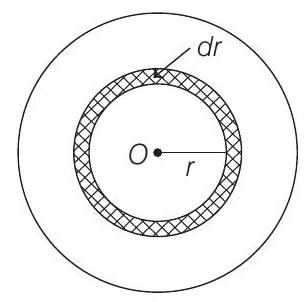
Moment of inertia about the axis of the disc,
From Eqs. (i) and (ii), we get






