Rotation 1 Question 17
20. Let
(a)
(b)
(c)
(d)
Objective Question II (One or more correct option)
Show Answer
Answer:
Correct Answer: 20. (a)
Solution:
From symmetry
and
From theorem of perpendicular axes,
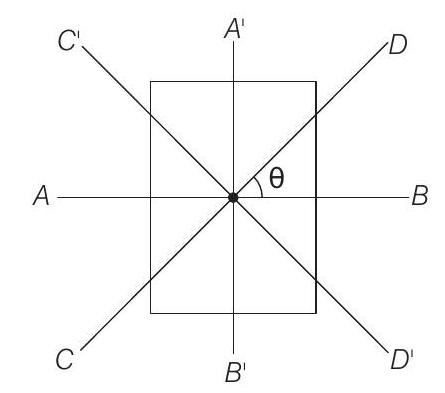
Alternate
The relation between
At
Similarly, at
Keeping these things in mind, only option (a) is correct.






