SATHEE: Rotation 1 Question 17

Rotation 1 Question 17

20. Let $I$ be the moment of inertia of a uniform square plate about an axis $A B$ that passes through its centre and is parallel to two of its sides. $C D$ is a line in the plane of the plate that passes through the centre of the plate and makes an angle $θ$ with $A B$ . The moment of inertia of the plate about the axis $C D$ is then equal to

(a) $I$

(b) $I \sin^{2} θ$

(d) $I \cos^{2} (θ / 2)$

$(1998, 2 M)$

Objective Question II (One or more correct option)

Show Answer

Answer:

Correct Answer: 20. (a)

Solution:

$A^{'} B^{'} ⊥ A B$ and $C^{'} D^{'} ⊥ C D$

From symmetry $I_{A B} = I_{A}^{'} B^{'}$

and

$I_{C D} = I_{C^{'} D^{'}}$

From theorem of perpendicular axes,

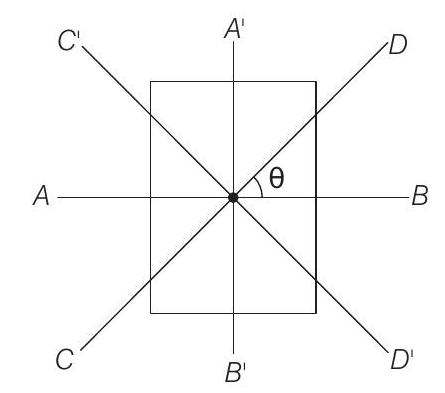
$\begin{aligned} I_{Z Z} = I_{A B} + I_{A^{'} B^{'}} & = I_{C D} + I_{C^{'} D^{'}} \\ = 2 I_{A B} = 2 I_{C D} \\ I_{A B} & = I_{C D} \end{aligned}$

Alternate

The relation between $I_{A B}$ and $I_{C D}$ should be true for all values of $θ$

$θ = 0, I_{C D} = I_{A B}$

Similarly, at $θ = π / 2, I_{C D} = I_{A B}$ (by symmetry)

Keeping these things in mind, only option (a) is correct.

पिछला

अगला

Rotation 1 Question 17

Objective Question II (One or more correct option)

Answer:

Alternate

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Rotation 1 Question 17

Objective Question II (One or more correct option)

Answer:

Alternate

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu