Rotation 1 Question 13
16. A solid sphere of radius $R$ has moment of inertia $I$ about its geometrical axis. It is melted into a disc of radius $r$ and thickness $t$. If it’s moment of inertia about the tangential axis (which is perpendicular to plane of the disc),
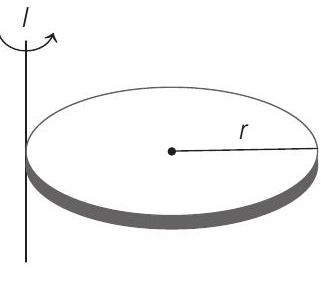is also equal to $I$, then the value of $r$ is equal to
(a) $\frac{2}{\sqrt{15}} R$
(b) $\frac{2}{\sqrt{5}} R$
(c) $\frac{3}{\sqrt{15}} R$
(d) $\frac{\sqrt{3}}{\sqrt{15}} R$
Show Answer
Answer:
Correct Answer: 16. (a)
Solution:
- $\quad \frac{2}{5} M R^{2}=\frac{1}{2} M r^{2}+M r^{2}$
or $\quad \frac{2}{5} M R^{2}=\frac{3}{2} M r^{2}$
$\therefore \quad r=\frac{2}{\sqrt{15}} R$
$$ \begin{aligned} I & =\frac{m a^{2}}{6}=\frac{\frac{2}{\sqrt{3} \pi} M \frac{2}{\sqrt{3}} R^{2}}{\sigma} \\ & =\frac{4 M R^{2}}{9 \sqrt{3} \pi} \end{aligned} $$
