Properties of Matter 4 Question 2
4. A glass capillary tube is of the shape of truncated cone with an apex angle $\alpha$ so that its two ends have cross-sections of different radii. When dipped in water vertically, water rises in it to a height $h$, where the radius of its cross-section is $b$. If the surface tension of water is $S$, its density is $\rho$, and its contact angle with glass is $\theta$, the value of $h$ will be ( $g$ is the acceleration due to gravity)
(2014 Adv.)
(a) $\frac{2 S}{b \rho g} \cos (\theta-\alpha)$
(b) $\frac{2 S}{b \rho g} \cos (\theta+\alpha)$
(c) $\frac{2 S}{b \rho g} \cos (\theta-\alpha / 2)$
(d) $\frac{2 S}{b \rho g} \cos (\theta+\alpha / 2)$
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Let $R$ be the radius of the meniscus formed with a contact angle $\theta$. By geometry, this radius makes an angle $\theta+\frac{\alpha}{2}$ with the horizontal and,
$$ \cos \left(\theta+\frac{\alpha}{2}\right)=b / R \cdots(i) $$
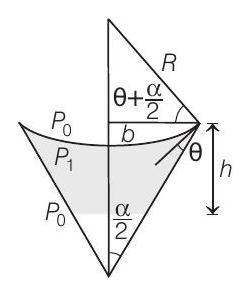
Let $P _0$ be the atmospheric pressure and $P _1$ be the pressure just below the meniscus. Excess pressure on the concave side of meniscus of radius $R$ is,
$$ P _0-P _1=2 S / R \cdots(ii) $$
The hydrostatic pressure gives,
$$ P _0-P _1=h \rho g \cdots(iii) $$
Eliminate $\left(P _0-P _1\right)$ from second and third equations and substitute $R$ from first equation to get,
$$ h=\frac{2 S}{\rho g R}=\frac{2 S}{b \rho g} \cos \left(\theta+\frac{\alpha}{2}\right) $$






