Properties of Matter 4 Question 2
4. A person in a lift is holding a water jar, which has a small hole at the lower end of its side. When the lift is at rest, the water jet coming out of the hole hits the floor of the lift at a distance
(2014 Adv.)
| List I | List II | ||
|---|---|---|---|
| A | Lift is accelerating vertically up. | ||
| B | Lift is accelerating vertically down with an acceleration less than the gravitational acceleration. |
||
| C | Lift is moving vertically up with constant speed. |
||
| No water leaks out of D |
Codes
(a) A-q, B-r, C-q, D-s
(b) A-q, B-r, C-p, D-s
(c) A-p, B-p, C-p, D-s
(d) A-q, B-r, C-p, D-p
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- Let
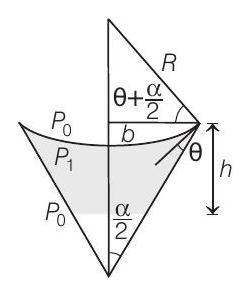
Let
The hydrostatic pressure gives,
Eliminate






