Properties of Matter 3 Question 8
14. A container of large uniform cross-sectional area $A$ resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities $d$ and $2 d$, each of height $H / 2$ as shown in figure. The lower density liquid is open to the atmosphere having pressure $p_0 .$
$(1995,5+5 \mathrm{M})$
(a) A homogeneous solid cylinder of length $L(L<H / 2)$, cross-sectional area $A / 5$ is immersed such that it floats with its axis vertical at the liquid-liquid interface with length $L / 4$ in the denser liquid. Determine
(i) the density $D$ of the solid,
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area $s(s«A)$ is punched on the vertical side of the container at a height $h(h<H / 2)$. Determine :
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance $x$ travelled by the liquid initially, and
(iii) the height $h_m$ at which the hole should be punched so that the liquid travels the maximum distance $x_m$ initially. Also calculate $x_m$.
(Neglect the air resistance in these calculations)
Show Answer
Answer:
Correct Answer: 14. (a) (i) $\frac{5 d}{4}$
(ii) $p=p _0+\frac{d g(6 H+L)}{4}$
(b) (i) $\sqrt{(3 H-4 h) \frac{g}{2}}$
(ii) $\sqrt{h(3 H-4 h)}$
(iii) At $h=\frac{3 H}{8} ; \frac{3}{4} H$
Solution:
- (a) (i) Considering vertical equilibrium of cylinder Weight of cylinder $=$ upthrust due to upper liquid + upthrust due to lower liquid
$$ \begin{aligned} & \therefore\left(\frac{A}{5}\right)(L) D \cdot g=\left(\frac{A}{5}\right)\left(\frac{3 L}{4}\right)(d) g+\left(\frac{A}{5}\right)\left(\frac{L}{4}\right)(2 d)(g) \\ & \therefore \quad D=\left(\frac{3}{4}\right) d+\left(\frac{1}{4}\right)(2 d) \\ & \Rightarrow D=\frac{5}{4} d \end{aligned} $$
(ii) Considering vertical equilibrium of two liquids and the cylinder.
$$ \left(p-p _0\right) A=\text { weight of two liquids } $$
+ weight of cylinder
$\therefore \frac{\text { weight of two liquids }+ \text { weight of cylinder }}{A} \cdots(i)$
Now, weight of cylinder
$$ =\left(\frac{A}{5}\right)(L)(D)(g)=\left(\frac{A}{5} L g\right)\left(\frac{5}{4} d\right)=\frac{A L d g}{4} $$
Weight of upper liquid $=\left(\frac{H}{2} A d g\right)$ and
Weight of lower liquid $=\frac{H}{2} A(2 d) g$
$$ =H A g d $$
$\therefore$ Total weight of two liquids $=\frac{3}{2} H A d g$
$\therefore$ From Eq. (i) pressure at the bottom of the container will be
$$ p=p _0+\frac{\left(\frac{3}{2}\right) H A d g+\frac{A L d g}{4}}{A} $$
or
$$ p=p _0+\frac{d g(6 H+L)}{4} $$
(b) (i) Applying Bernoulli’s theorem,
$$ \begin{array}{r} p _0+d g\left(\frac{H}{2}\right)+2 d g\left(\frac{H}{2}-h\right) \\ =p _0+\frac{1}{2}(2 d) v^{2} \end{array} $$
Here, $v$ is velocity of efflux at 2 . Solving this, we get
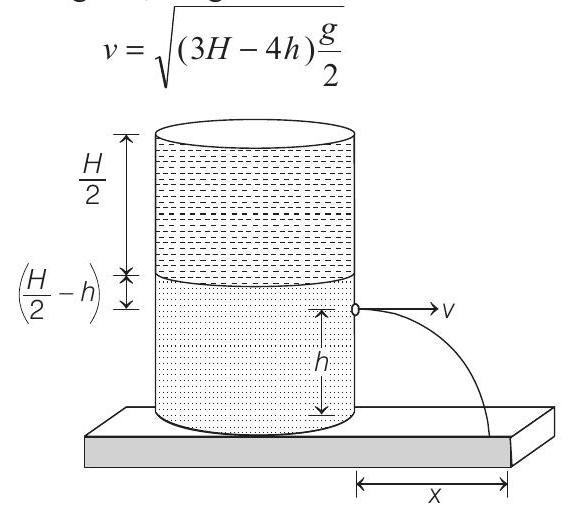
(ii) Time taken to reach the liquid to the bottom will be
$$ t=\sqrt{2 h / g} $$
$\therefore$ Horizontal distance $x$ travelled by the liquid is
$$ \begin{aligned} & x=v t=\sqrt{\left.(3 H-4 h) \frac{g}{2}\right)}\left(\sqrt{\frac{2 h}{g}}\right) \\ & x=\sqrt{h(3 H-4 h)} \end{aligned} $$
(iii) For $x$ to be maximum $\frac{d x}{d h}=0$
$$ \begin{array}{ll} \text { or } & \frac{1}{2 \sqrt{h(3 H-4 h)}}(3 H-8 h)=0 \\ \text { or } & h=\frac{3 H}{8} \end{array} $$
Therefore, $x$ will be maximum at $h=\frac{3 H}{8}$
The maximum value of $x$ will be
$$ \begin{aligned} & x _m=\sqrt{\left(\frac{3 H}{8}\right)\left[3 H-4\left(\frac{3 H}{8}\right)\right]} \\ & x _m=\frac{3}{4} H \end{aligned} $$






