SATHEE: Properties of Matter 3 Question 8

Properties of Matter 3 Question 8

14. Consider two solid spheres $P$ and $Q$ each of density $8 g m c m^{- 3}$ and diameters $1 c m$ and $0.5 c m$ , respectively. Sphere $P$ is dropped into a liquid of density $0.8 g m c m^{- 3}$ and viscosity $η = 3$ poiseulles. Sphere $Q$ is dropped into a liquid of density $1.6 g m c m^{- 3}$ and viscosity $η = 2$ poiseulles. The ratio of the terminal velocities of $P$ and $Q$ is

(2016 Adv.)

Show Answer

Answer:

Correct Answer: 14. (a) (i) $\frac{5 d}{4}$

(ii) $p = p_{0} + \frac{d g (6 H + L)}{4}$ (b) (i) $\sqrt{(3 H - 4 h) \frac{g}{2}}$ (ii) $\sqrt{h (3 H - 4 h)}$ (iii) At $h = \frac{3 H}{8}; \frac{3}{4} H$

Solution:

(a) (i) Considering vertical equilibrium of cylinder Weight of cylinder $=$ upthrust due to upper liquid + upthrust due to lower liquid

$\begin{aligned} ∴ (\frac{A}{5}) (L) D \cdot g = (\frac{A}{5}) (\frac{3 L}{4}) (d) g + (\frac{A}{5}) (\frac{L}{4}) (2 d) (g) \\ ∴ D = (\frac{3}{4}) d + (\frac{1}{4}) (2 d) \\ \Rightarrow D = \frac{5}{4} d \end{aligned}$

(ii) Considering vertical equilibrium of two liquids and the cylinder.

$(p - p_{0}) A = weight of two liquids$

weight of cylinder

$∴ \frac{weight of two liquids + weight of cylinder}{A}$

Now, weight of cylinder

$= (\frac{A}{5}) (L) (D) (g) = (\frac{A}{5} L g) (\frac{5}{4} d) = \frac{A L d g}{4}$

Weight of upper liquid $= (\frac{H}{2} A d g)$ and

Weight of lower liquid $= \frac{H}{2} A (2 d) g$

$= H A g d$

$∴$ Total weight of two liquids $= \frac{3}{2} H A d g$

$∴$ From Eq. (i) pressure at the bottom of the container will be

$p = p_{0} + \frac{(\frac{3}{2}) H A d g + \frac{A L d g}{4}}{A}$

$p = p_{0} + \frac{d g (6 H + L)}{4}$

(b) (i) Applying Bernoulli’s theorem,

$\begin{array}{r} p_{0} + d g (\frac{H}{2}) + 2 d g (\frac{H}{2} - h) \\ = p_{0} + \frac{1}{2} (2 d) v^{2} \end{array}$

Here, $v$ is velocity of efflux at 2 . Solving this, we get

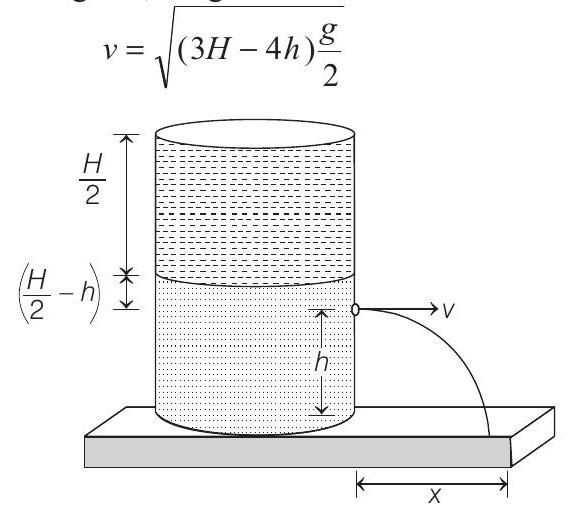
(ii) Time taken to reach the liquid to the bottom will be

$t = \sqrt{2 h / g}$

$∴$ Horizontal distance $x$ travelled by the liquid is

$\begin{aligned} x = v t = \sqrt{(3 H - 4 h) \frac{g}{2})} (\sqrt{\frac{2 h}{g}}) \\ x = \sqrt{h (3 H - 4 h)} \end{aligned}$

(iii) For $x$ to be maximum $\frac{d x}{d h} = 0$

$\begin{array}{ll} or & \frac{1}{2 \sqrt{h (3 H - 4 h)}} (3 H - 8 h) = 0 \\ or & h = \frac{3 H}{8} \end{array}$

Therefore, $x$ will be maximum at $h = \frac{3 H}{8}$

The maximum value of $x$ will be

$\begin{aligned} x_{m} = \sqrt{(\frac{3 H}{8}) [3 H - 4 (\frac{3 H}{8})]} \\ x_{m} = \frac{3}{4} H \end{aligned}$

पिछला

अगला

Properties of Matter 3 Question 8

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Properties of Matter 3 Question 8

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu