Optics 7 Question 43
44. Two parallel beams of light $P$ and $Q$ (separation $d$ ) containing radiations of wavelengths $4000 \AA$ and $5000 \AA$ (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure.
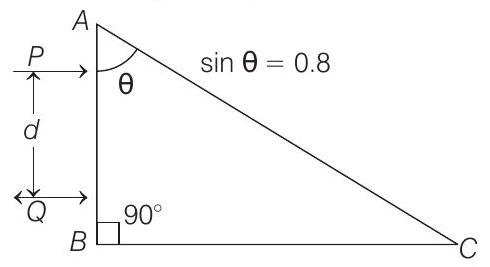
The refractive index of the prism as a function of wavelength is given by the relation, $\mu(\lambda)=1.20+\frac{b}{\lambda^{2}}$ where $\lambda$ is in $\AA$ and $b$ is positive constant. The value of $b$ is such that the condition for total reflection at the face $A C$ is just satisfied for one wavelength and is not satisfied for the other.
$(1991,2+2+4 M)$
(a) Find the value of $b$.
(b) Find the deviation of the beams transmitted through the face $A C$.
(c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of the upper and the lower beams immediately after transmission from the face $A C$, are $4 I$ and $I$ respectively, find the resultant intensity at the focus.
Show Answer
Answer:
Correct Answer: 44. (a) $b=8 \times 10^{5}(\AA)^{2}$ (b) $\delta _{4000 \AA}=37^{\circ}, \delta _{5000 \AA}=27.13^{\circ}$ (c) $9 I$
Solution:
- (a) Total internal reflection (TIR) will take place first for that wavelength for which critical angle is small or $\mu$ is large.
From the given expression of $\mu$, it is more for the wavelength for which value
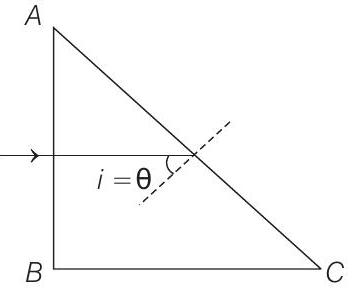of $\lambda$ is less.
Thus, condition of TIR is just satisfied for $4000 \AA$.
or $i=\theta _c$ for $4000 \AA$ or $\theta=\theta _c$ or $\sin \theta=\sin \theta _c$
$$ \begin{aligned} & \text { or } 0.8=\frac{1}{\mu} \\ & \text { or } 0.8=\frac{1}{1.20+\frac{b}{(4000)^{2}}} \end{aligned} $$
Solving this equation, we get $b=8.0 \times 10^{5}(\AA)^{2}$
(b)
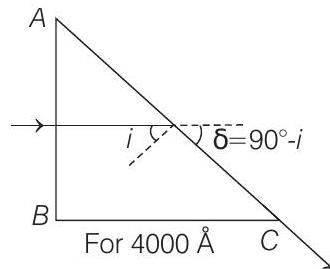
For, $4000 \AA$ condition of TIR is just satisfied. Hence, it will emerge from $A C$, just grazingly.
or $\delta _{4000 \AA}=90^{\circ}-i=90^{\circ}-\sin ^{-1}(0.8) \approx 37^{\circ}$
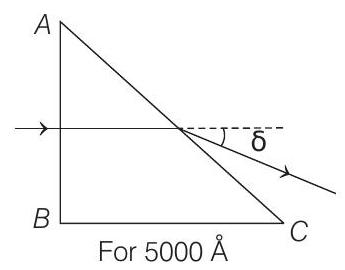
For $5000 \AA \mu=1.2+\frac{b}{\lambda^{2}}=1.2+\frac{8.0 \times 10^{5}}{(5000)^{2}}=1.232$
Applying $\mu=\frac{\sin i _{\text {air }}}{\sin i _{\text {medium }}} \quad$ or $\quad 1.232=\frac{\sin i _{\text {air }}}{\sin \theta}$
$$ \begin{aligned} & =\frac{\sin i _{\text {air }}}{0.8} \Rightarrow i _{\text {air }}=80.26^{\circ} \\ \therefore \quad \delta _{5000 \AA} & =i _{\text {air }}-i _{\text {medium }} \\ & =80.26^{\circ}-\sin ^{-1}(0.8)=27.13^{\circ} \end{aligned} $$
(c)
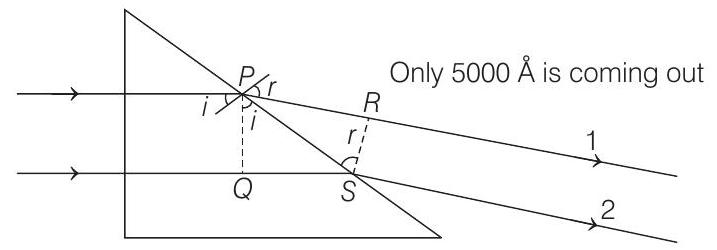
Path difference between rays 1 and 2
$\Delta x=\mu(Q S)-P R$
Further, $\quad \frac{Q S}{P S}=\sin i \Rightarrow \frac{P R}{P S}=\sin r$
$\therefore \quad \frac{P R / P S}{Q S / P S}=\frac{\sin r}{\sin i}=\mu \Rightarrow \mu(Q S)=P R$
Substituting in Eq. (i), we get $\Delta x=0$.
$\therefore$ Phase difference between rays 1 and 2 will be zero.
Or these two rays will interfere constructively. So, maximum intensity will be obtained from their interference.
$$ \text { or } $$
$$ I _{\max }=\left(\sqrt{I _1}+\sqrt{I _2}\right)^{2}=(\sqrt{4 I}+\sqrt{I})^{2}=9 I $$
NOTE In this question we have written,
$$ \mu=\frac{\sin r}{\sin i} \text { not } \frac{\sin i}{\sin r} $$
because in medium angle with normal is $i$ and in air angle with normal is $r$.
or
$$ \mu=\frac{\sin i _{\text {air }}}{\sin i _{\text {medium }}} $$
