SATHEE: Optics 7 Question 43

Optics 7 Question 43

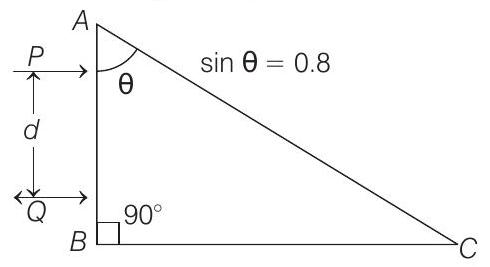
44. Two parallel beams of light $P$ and $Q$ (separation $d$ ) containing radiations of wavelengths $4000 \AA$ and $5000 \AA$ (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure.

The refractive index of the prism as a function of wavelength is given by the relation, $μ (λ) = 1.20 + \frac{b}{λ^{2}}$ where $λ$ is in $\AA$ and $b$ is positive constant. The value of $b$ is such that the condition for total reflection at the face $A C$ is just satisfied for one wavelength and is not satisfied for the other.

$(1991, 2 + 2 + 4 M)$

(a) Find the value of $b$ .

(b) Find the deviation of the beams transmitted through the face $A C$ .

(c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of the upper and the lower beams immediately after transmission from the face $A C$ , are $4 I$ and $I$ respectively, find the resultant intensity at the focus.

Show Answer

Answer:

Correct Answer: 44. (a) $b = 8 \times 10^{5} (\AA)^{2}$ (b) $δ_{4000 \AA} = 37^{\circ}, δ_{5000 \AA} = {27.13}^{\circ}$ (c) $9 I$

Solution:

(a) Total internal reflection (TIR) will take place first for that wavelength for which critical angle is small or $μ$ is large.

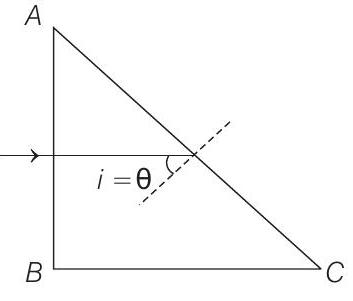From the given expression of $μ$ , it is more for the wavelength for which value

of $λ$ is less.

Thus, condition of TIR is just satisfied for $4000 \AA$ .

or $i = θ_{c}$ for $4000 \AA$ or $θ = θ_{c}$ or $\sin θ = \sin θ_{c}$

$\begin{aligned} or 0.8 = \frac{1}{μ} \\ or 0.8 = \frac{1}{1.20 + \frac{b}{(4000)^{2}}} \end{aligned}$

Solving this equation, we get $b = 8.0 \times 10^{5} (\AA)^{2}$

(b)

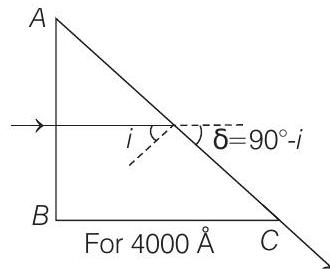
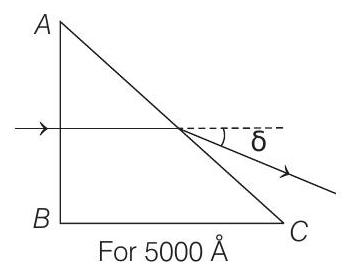
For, $4000 \AA$ condition of TIR is just satisfied. Hence, it will emerge from $A C$ , just grazingly.

or $δ_{4000 \AA} = 90^{\circ} - i = 90^{\circ} - \sin^{- 1} (0.8) \approx 37^{\circ}$

For $5000 \AA μ = 1.2 + \frac{b}{λ^{2}} = 1.2 + \frac{8.0 \times 10^{5}}{(5000)^{2}} = 1.232$

Applying $μ = \frac{\sin i_{air}}{\sin i_{medium}}$ or $1.232 = \frac{\sin i_{air}}{\sin θ}$

$\begin{aligned} = \frac{\sin i_{air}}{0.8} \Rightarrow i_{air} = {80.26}^{\circ} \\ ∴ δ_{5000 \AA} & = i_{air} - i_{medium} \\ = {80.26}^{\circ} - \sin^{- 1} (0.8) = {27.13}^{\circ} \end{aligned}$

(c)

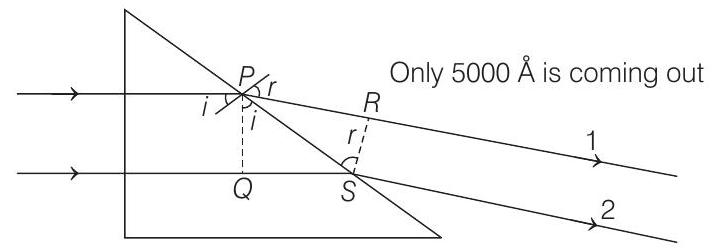
Path difference between rays 1 and 2

$Δ x = μ (Q S) - P R$

Further, $\frac{Q S}{P S} = \sin i \Rightarrow \frac{P R}{P S} = \sin r$

$∴ \frac{P R / P S}{Q S / P S} = \frac{\sin r}{\sin i} = μ \Rightarrow μ (Q S) = P R$

Substituting in Eq. (i), we get $Δ x = 0$ .

$∴$ Phase difference between rays 1 and 2 will be zero.

Or these two rays will interfere constructively. So, maximum intensity will be obtained from their interference.

$or$

$I_{max} = {(\sqrt{I_{1}} + \sqrt{I_{2}})}^{2} = (\sqrt{4 I} + \sqrt{I})^{2} = 9 I$

NOTE In this question we have written,

$μ = \frac{\sin r}{\sin i} not \frac{\sin i}{\sin r}$

because in medium angle with normal is $i$ and in air angle with normal is $r$ .

$μ = \frac{\sin i_{air}}{\sin i_{medium}}$

पिछला

अगला

Optics 7 Question 43

44. Two parallel beams of light $P$ and $Q$ (separation $d$ ) containing radiations of wavelengths $4000 \AA$ and $5000 \AA$ (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Optics 7 Question 43

44. Two parallel beams of light P and Q (separation d ) containing radiations of wavelengths 4000\AA and 5000\AA (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

44. Two parallel beams of light $P$ and $Q$ (separation $d$ ) containing radiations of wavelengths $4000 \AA$ and $5000 \AA$ (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure.