Optics 7 Question 38
39. A thin biconvex lens of refractive index $3 / 2$ is placed on a horizontal plane mirror as shown in the figure. The space between the lens and the mirror is then filled with water of refractive index $4 / 3$. It is found that when a point object is placed $15 cm$ above the lens on its principal axis, the object coincides with its own image. On repeating with another liquid, the object and the image again coincide at a distance $25 cm$ from the lens. Calculate the refractive index of the liquid.
$(2001,5$ M)

Show Answer
Solution:
- Let $R$ be the radius of curvature of both the surfaces of the equi-convex lens. In the first case :
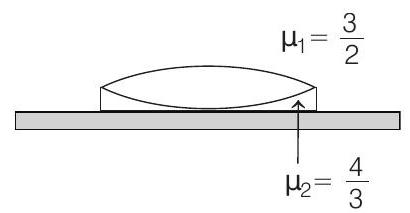
Let $f _1$ be the focal length of equi-convex lens of refractive index $\mu _1$ and $f _2$ the focal length of plano-concave lens of refractive index $\mu _2$. The focal length of the combined lens system will be given by
$$ \begin{aligned} \frac{1}{F} & =\frac{1}{f _1}+\frac{1}{f _2} \\ & =\left(\mu _1-1\right) \frac{1}{R}-\frac{1}{-R}+\left(\mu _2-1\right) \frac{1}{-R}-\frac{1}{\infty} \\ & =\frac{3}{2}-1 \quad \frac{2}{R}+\frac{4}{3}-1-\frac{1}{R} \\ & =\frac{1}{R}-\frac{1}{3 R}=\frac{2}{3 R} \text { or } F=\frac{3 R}{2} \end{aligned} $$
Now, image coincides with the object when ray of light retraces its path or it falls normally on the plane mirror. This is possible only when object is at focus of the lens system.
Hence, $F=15 cm$ (Distance of object $=15 cm$ )
or $\quad \frac{3 R}{2}=15 cm$ or $R=10 cm$
In the second case, let $\mu$ be the refractive index of the liquid filled between lens and mirror and let $F^{\prime}$ be the focal length of new lens system. Then,
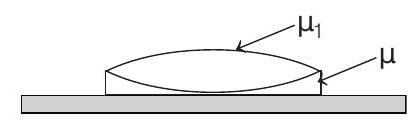
$$ \begin{array}{rlrl} \frac{1}{F^{\prime}} & =\left(\mu _1-1\right) \frac{1}{R}-\frac{1}{-R}+(\mu-1) \frac{1}{-R}-\frac{1}{\infty} \\ \text { or } & \frac{1}{F^{\prime}} & =\frac{3}{2}-1 \frac{2}{R}-\frac{(\mu-1)}{R} & \\ \text { or } & & =\frac{1}{R}-\frac{\mu-1}{R}=\frac{(2-\mu)}{R} \\ \therefore & F^{\prime} & =\frac{R}{2-\mu}=\frac{10}{2-\mu} \quad(\because R=10 cm) \end{array} $$
Now, the image coincides with object when it is placed at $25 cm$ distance.
$$ \begin{array}{rlrl} \text { Hence, } & F^{\prime} & =25 \\ \text { or } & \frac{10}{2-\mu} & =25 \\ \text { or } & 50-25 \mu & =10 \\ \text { or } & 25 \mu & =40 \\ \therefore & \mu=\frac{40}{25} & =1.6 \\ \text { or } & \mu=1.6 \end{array} $$






