Optics 7 Question 38
39. A thin biconvex lens of refractive index

Show Answer
Solution:
- Let
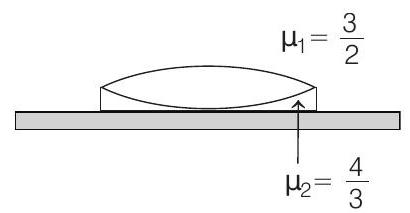
Let
Now, image coincides with the object when ray of light retraces its path or it falls normally on the plane mirror. This is possible only when object is at focus of the lens system.
Hence,
or
In the second case, let
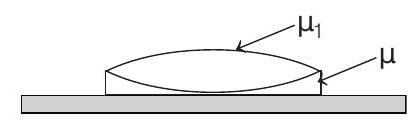
Now, the image coincides with object when it is placed at






