Optics 4 Question 11
11. An isosceles prism of angle $120^{\circ}$ has a refractive index 1.44. Two parallel rays of monochromatic light enter the prism parallel to each other in air as shown. The rays emerging from the opposite face
$(1995,2 M)$
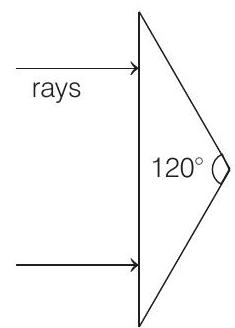
(a) are parallel to each other
(b) are diverging
(c) make an angle $2\left[\sin ^{-1}(0.72)-30^{\circ}\right]$ with each other
(d) make an angle $2 \sin ^{-1}(0.72)$ with each other
Show Answer
Answer:
Correct Answer: 11. (c)
Solution:
- The diagramatic representation of the given problem is shown in figure.
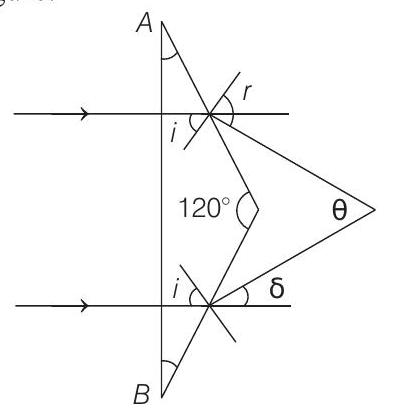
From figure it follows that $\angle i=\angle A=30^{\circ}$
From Snell’s law, $n _1 \sin i=n _2 \sin r$
or $\quad \sin r=\frac{1.44 \sin 30^{\circ}}{1}=0.72$
Now, $\quad \angle \delta=\angle r-\angle i=\sin ^{-1}(0.72)-30^{\circ}$
$\therefore \quad \theta=2(\angle \delta)=2{\sin ^{-1}(0.72)-30^{\circ}}$
