Optics 3 Question 2
2. A thin convex lens $L$ (refractive index $=1.5)$ is placed on a plane mirror $M$. When a pin is placed at $A$, such that $O A=18 cm$, its real inverted image is formed at $A$ itself, as shown in figure. When a liquid of refractive index $\mu _l$ is put between the lens and the mirror, the pin has to be moved to $A^{\prime}$, such that $O A^{\prime}=27 cm$, to get its inverted real image at $A^{\prime}$ itself. The value of $\mu _l$ will be
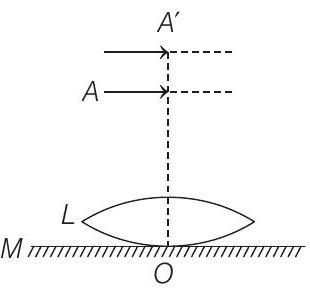
(a) $\sqrt{3}$
(b) $\sqrt{2}$
(c) $\frac{4}{3}$
(d) $\frac{3}{2}$
(2019 Main, 9 April II)
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
- Light from plane mirror is reflected back on it’s path, so that image of $A$ coincides with $A$ itself.
This would happen when rays refracted by the convex lens falls normally on the plane mirror, i.e.
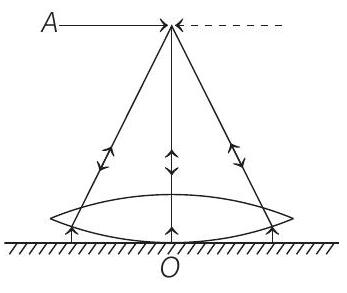the refracted rays form a beam parallel to principal axis of the lens. Hence, the object would then be considered at the focus of convex lens.
$\therefore$ Focal length of curvature of convex lens is, $f _1=18 cm$
With liquid between lens and mirror, image is again coincides with object, so the second measurement is focal length of combination of liquid lens and convex lens.
$\therefore \frac{1}{f _1}+\frac{1}{f _2}=\frac{1}{f _{\text {eq }}} \Rightarrow \frac{1}{18}+\frac{1}{f _2}=\frac{1}{27} \Rightarrow f _2=-54 cm$
For convex lens by lens maker’s formula, we have
$$ \frac{1}{f}=(\mu-1) \frac{2}{R} \Rightarrow \frac{1}{18}=0.5 \times \frac{2}{R} \Rightarrow R=18 cm $$
and for plano-convex liquid lens, we have
$$ \begin{aligned} \frac{1}{f} & =\left(\mu _l-1\right) \frac{-1}{R} \Rightarrow-\frac{1}{54}=\left(\mu _l-1\right) \frac{-1}{18} \\ \Rightarrow \mu _l & =1+\frac{1}{3}=\frac{4}{3} \end{aligned} $$
