Optics 3 Question 2
2. A thin convex lens
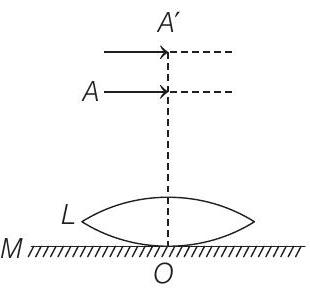to be moved to
(a)
(b)
(c)
(d)
(2019 Main, 9 April II)
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
- Light from plane mirror is reflected back on it’s path, so that image of
This would happen when rays refracted by the convex lens falls normally on the plane mirror, i.e.
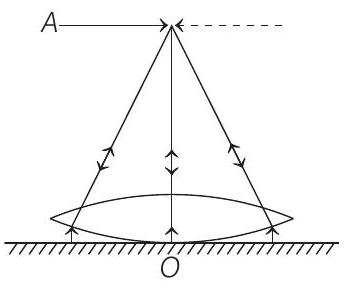the refracted rays form a beam parallel to principal axis of the lens. Hence, the object would then be considered at the focus of convex lens.
With liquid between lens and mirror, image is again coincides with object, so the second measurement is focal length of combination of liquid lens and convex lens.
For convex lens by lens maker’s formula, we have
and for plano-convex liquid lens, we have
