Optics 1 Question 13
13. A thin rod of length $f / 3$ is placed along the optic axis of a concave mirror of focal length $f$ such that its image which is real and elongated, just touches the rod. The magnification is ……
(1991, 1M)
Show Answer
Answer:
Correct Answer: 13. $(-1.5)$
Solution:
- $F=$ focus, $C=$ centre of curvature
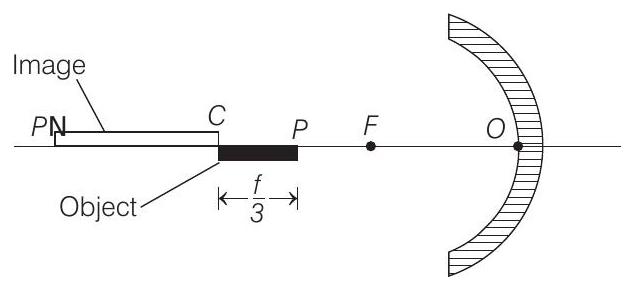
When the object lies between $F$ and $C$, image is real, elongated and inverted. As one end of rod just touches its image, this end should lie at $C$. Because image of object at $C$ is at $C$ itself.
Let $P^{\prime}$ be the image of other end of $\operatorname{rod} P$.
For $P$
$$ u=-(2 f-f / 3)=-\frac{5 f}{3} $$
Applying the mirror formula $: \frac{1}{v}+\frac{1}{u}=\frac{1}{f}$
$$ \begin{aligned} & \text { or } \quad \frac{1}{v}-\frac{3}{5 f}=\frac{1}{-f} \Rightarrow \frac{1}{v}=\frac{3}{5 f}-\frac{1}{f} \\ & \text { or } \quad v=-\frac{5 f}{2} \quad \text { or } \quad O P^{\prime}=\frac{5 f}{2} \end{aligned} $$
$\therefore$ Length of image of rod
$$ \begin{aligned} & C P^{\prime}=O P^{\prime}-O C=\frac{5 f}{2}-2 f=\frac{f}{2} \\ \therefore \quad & \text { Magnification }=-\frac{f / 2}{f / 3}=-1.5 \end{aligned} $$
Here, negative sign implies that image is inverted.






