Optics 1 Question 13
13. A thin rod of length
(1991, 1M)
Integer Answer Type Question
Show Answer
Answer:
Correct Answer: 13.
Solution:
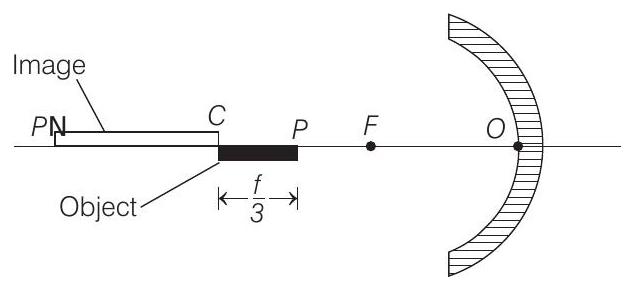
When the object lies between
Let
For
Applying the mirror formula
Here, negative sign implies that image is inverted.






