Modern Physics 6 Question 11
11. The circuit shown below contains two ideal diodes, each with a forward resistance of $50 \Omega$. If the battery voltage is $6 V$, the current through the $100 \Omega$ resistance (in ampere) is
(Main 2019, 11 Jan II)
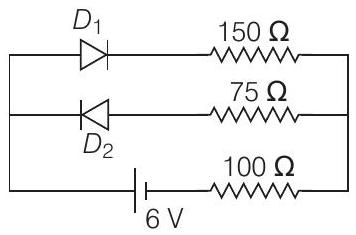
(a) 0.027
(b) 0.020
(c) 0.030
(d) 0.036
Show Answer
Solution:
- In this circuit, $D _1$ is forward biased and $D _2$ is reversed biased.
Resistance of $D _1$ is $50 \Omega$.
$\therefore$ Net resistance of the circuit,
$$ R _{\text {net }}=50+150+100=300 \Omega $$
$\therefore$ Current through the $100 \Omega$ resistance
$$ =\frac{V}{R _{\text {net }}}=\frac{6}{300}=0.020 A $$
Key Idea When the applied reverse voltage $(V)$ reaches the breakdown voltage of the Zener diode, then only a large amount of current is flown through it, otherwise it is approximately zero.
In the given situation, if we consider that Zener diode is at breakdown. Then, potential drop across $1500 \Omega$ resistances will be $10 V$. So potential drop at $500 \Omega$ resistor will be $2 V$.
$\therefore$ Current in $R _1=\frac{2}{500}=4 mA=I _1$ (say)
Current in each
$$ \begin{aligned} & R _2=\frac{10}{750}=\frac{2}{150}=13.33 mA=I _2 \text { (say) } \\ \Rightarrow & I _1<I _2 \text { which is not possible. } \end{aligned} $$
So, Zener diode will never reach to its breakdown.
$\therefore$ Current flowing through a reverse biased Zener diode $=0$






