Modern Physics 6 Question 11
11. The circuit shown below contains two ideal diodes, each with a forward resistance of
(Main 2019, 11 Jan II)
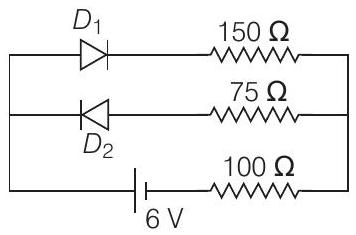
(a) 0.027
(b) 0.020
(c) 0.030
(d) 0.036
Show Answer
Solution:
- In this circuit,
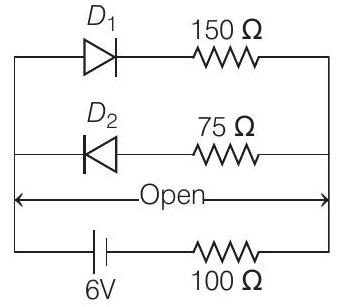
Resistance of
Key Idea When the applied reverse voltage
In the given situation, if we consider that Zener diode is at breakdown. Then, potential drop across
Current in each
So, Zener diode will never reach to its breakdown.






