Modern Physics 5 Question 1
1. Half lives of two radioactive nuclei $A$ and $B$ are 10 minutes and 20 minutes, respectively. If initially a sample has equal number of nuclei, then after
60 minutes, the ratio of decayed numbers of nuclei $A$ and $B$ will be
(Main 2019, 12 April II)
(a) $3: 8$
(b) $1: 8$
(c) $8: 1$
(d) $9: 8$
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- For substance $A$, half-life is $10 min$, so it decays as
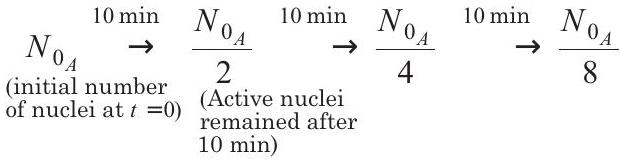
$$ \begin{aligned} & \stackrel{10 \min }{\rightarrow} \frac{N _{0 _A}}{16} \stackrel{10 min}{\rightarrow} \frac{N _{0 _A}}{32} \quad 10 min \rightarrow \frac{N _{0 _A}}{64} \end{aligned} $$
$\therefore$ For substance $A$, number of nuclei decayed in $60 min$ is
$$ N _{0 _A}-\frac{N _{0 _A}}{64}=\frac{63 N _{0 _A}}{64} $$
Similarly, for substance $B$, half-life is $20 min$, so it’s decay scheme is
$$ N _{0 _B} \stackrel{20 min}{\rightarrow} \frac{N _{0 _B}}{2} \stackrel{20 min}{\rightarrow} \frac{N _{0 _B}}{4} \stackrel{20 min}{\rightarrow} \frac{N _{0 _B}}{8} $$
So, number of nuclei of $B$ decayed in $60 min$ is
$$ N _{0 _B}-\frac{N _{0 _B}}{8}=\frac{7}{8} N _{0 _B} $$
Hence, ratio of decayed nuclei of $A$ and $B$ in $60 min$ is
$$ \frac{\frac{63}{64} N _{0 _A}}{\frac{7}{8} N _{0 _B}}=\frac{9}{8} \quad\left[\because N _{0 _A}=N _{0 _B}\right] $$
Alternate Solution
Number of active nuclei remained after $60 min$ can also be calculated as
$$ N^{\prime}=\frac{N}{2^{T / t _{1 / 2}}} $$
where, $T=60 min$
So, for nuclei $A$,
$$ N _{0 _A}^{\prime}=\frac{N _{0 _A}}{2^{\frac{60}{10}}}=\frac{N _{0 _A}}{2^{6}}=\frac{N _{0 _A}}{64} $$
Similarly, for nuclei $B$,
$$ N _{0 _B}^{\prime}=\frac{N _{0 _B}}{2^{\frac{60}{20}}}=\frac{N _{0 _B}}{2^{3}}=\frac{N _{0 _B}}{8} $$






