Magnetics 6 Question 20
20. Consider two different metallic strips (1 and 2) of same dimensions (length $l$, width $w$ and thickness $d$ ) with carrier densities $n _1$ and $n _2$, respectively. Strip 1 is placed in magnetic field $B _1$ and strip 2 is placed in magnetic field $B _2$, both along positive $y$-directions. Then $V _1$ and $V _2$ are the potential differences developed between $K$ and $M$ in strips 1 and 2, respectively. Assuming that the current $I$ is the same for both the strips, the correct options is/are
(2015 Adv.)
(a) If $B _1=B _2$ and $n _1=2 n _2$, then $V _2=2 V _1$
(b) If $B _1=B _2$ and $n _1=2 n _2$, then $V _2=V _1$
(c) If $B _1=2 B _2$ and $n _1=n _2$, then $V _2=0.5 V _1$
(d) If $B _1=2 B _2$ and $n _1=n _2$, then $V _2=V _1$
Passage 2
Electrical resistance of certain materials, known as superconductors, changes abruptly from a non-zero value to zero as their temperature is lowered below a critical temperature $T _C(0) . \quad$ An interesting property of superconductors
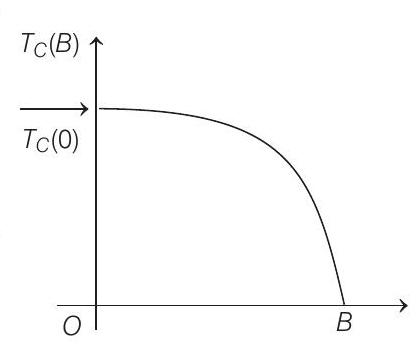 is that their critical temperature becomes smaller than $T _C(0)$ if they are placed in a magnetic field i.e. the critical temperature $T _C(B)$ is a function of the magnetic field strength $B$. The dependence of $T _C(B)$ on $B$ is shown in the figure.
is that their critical temperature becomes smaller than $T _C(0)$ if they are placed in a magnetic field i.e. the critical temperature $T _C(B)$ is a function of the magnetic field strength $B$. The dependence of $T _C(B)$ on $B$ is shown in the figure.
(2010)
Show Answer
Solution:
- $V=\frac{B I}{n e d} \Rightarrow \frac{V _1}{V _2}=\frac{B _1}{B _2} \times \frac{n _2}{n _1}$
If $B _1=B _2$ and $n _1=2 n _2$, then $V _2=2 V _1$
If $B _1=2 B _2$ and $n _1=n _2$, then $V _2=0.5 V _1$






