Magnetics 6 Question 20
20. Consider two different metallic strips (1 and 2) of same dimensions (length
(2015 Adv.)
(a) If
(b) If
(c) If
(d) If
Passage 2
Electrical resistance of certain materials, known as superconductors, changes abruptly from a non-zero value to zero as their temperature is lowered below a critical temperature
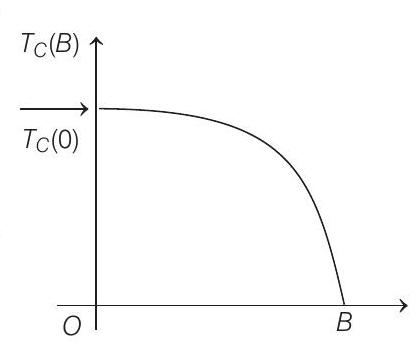is that their critical temperature becomes smaller than
(2010)
Show Answer
Solution:
If
If
