SATHEE: Magnetics 5 Question 5

Magnetics 5 Question 5

5. At some location on earth, the horizontal component of earth’s magnetic field is $18 \times 10^{- 6} T$ . At this location, magnetic needle of length $0.12 m$ and pole strength $1.8 A - m$ is suspended from its mid point using a thread, it makes $45^{\circ}$ angle with horizontal in equilibrium. To keep this needle horizontal, the vertical force that should be applied at one of its ends is

(a) $6.5 \times 10^{- 5} N$

(b) $3.6 \times 10^{- 5} N$

(d) $1.8 \times 10^{- 5} N$

(2019 Main, 10 Jan II)

Show Answer

Answer:

Correct Answer: 5. (a)

Solution:

Without applied forces, (in equilibrium position) the needle will stay in the resultant magnetic field of earth. Hence, the dip ’ $θ$ ’ at this place is $45^{\circ}$ (given).

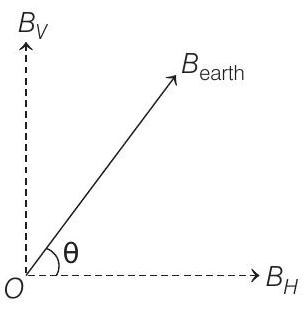
We know that, horizontal and vertical components of earth’s magnetic field ( $B_{H}$ and $B_{V})$ are related as

$\frac{B_{V}}{B_{H}} = \tan θ$

Here, $θ = 45^{\circ}$ and $B_{H} = 18 \times 10^{- 6} T$

$\begin{array}{ll} \Rightarrow & B_{V} = B_{H} \tan 45^{\circ} \\ \Rightarrow & B_{V} = B_{H} = 18 \times 10^{- 6} T (∵ \tan 45^{\circ} = 1) \end{array}$

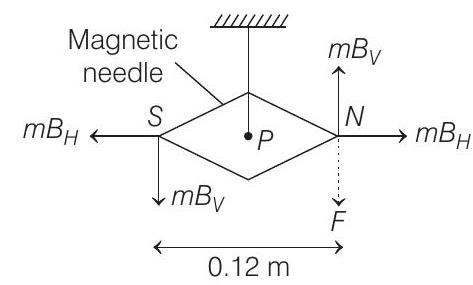
Now, when the external force $F$ is applied, so as to keep the needle stays in horizontal position is shown below,

Taking torque at point $P$ , we get

$\begin{array}{ll} m B_{V} \times 2 l = F l \\ ∴ & F = 2 \times m B_{V} \end{array}$

Substituting the given values, we get

$\begin{aligned} = 2 \times 1.8 \times 18 \times 10^{- 6} \\ = 6.48 \times 10^{- 5} = 6.5 \times 10^{- 5} N \end{aligned}$

Magnetics 5 Question 5

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Magnetics 5 Question 5

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu