Magnetics 5 Question 5
5. At some location on earth, the horizontal component of earth’s magnetic field is $18 \times 10^{-6} T$. At this location, magnetic needle of length $0.12 m$ and pole strength $1.8 A-m$ is suspended from its mid point using a thread, it makes $45^{\circ}$ angle with horizontal in equilibrium. To keep this needle horizontal, the vertical force that should be applied at one of its ends is
(a) $6.5 \times 10^{-5} N$
(b) $3.6 \times 10^{-5} N$
(c) $1.3 \times 10^{-5} N$
(d) $1.8 \times 10^{-5} N$
(2019 Main, 10 Jan II)
Show Answer
Answer:
Correct Answer: 5. (a)
Solution:
- Without applied forces, (in equilibrium position) the needle will stay in the resultant magnetic field of earth. Hence, the dip ’ $\theta$ ’ at this place is $45^{\circ}$ (given).
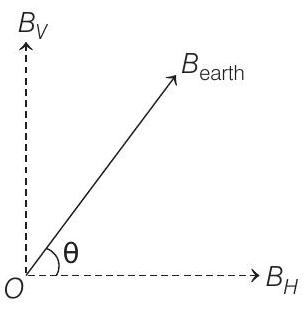
We know that, horizontal and vertical components of earth’s magnetic field ( $B _H$ and $\left.B _V\right)$ are related as
$$ \frac{B _V}{B _H}=\tan \theta $$
Here, $\theta=45^{\circ}$ and $B _H=18 \times 10^{-6} T$
$$ \begin{array}{ll} \Rightarrow & B _V=B _H \tan 45^{\circ} \\ \Rightarrow & B _V=B _H=18 \times 10^{-6} T \quad\left(\because \tan 45^{\circ}=1\right) \end{array} $$
Now, when the external force $F$ is applied, so as to keep the needle stays in horizontal position is shown below,
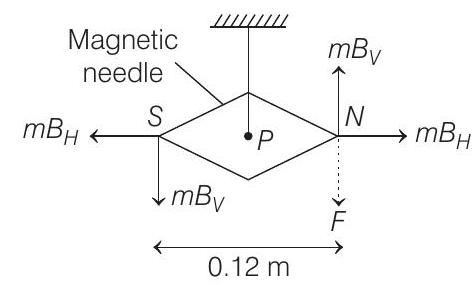
Taking torque at point $P$, we get
$$ \begin{array}{ll} & m B _V \times 2 l=F l \\ \therefore & F=2 \times m B _V \end{array} $$
Substituting the given values, we get
$$ \begin{aligned} & =2 \times 1.8 \times 18 \times 10^{-6} \\ & =6.48 \times 10^{-5}=6.5 \times 10^{-5} N \end{aligned} $$






