Magnetics 2 Question 10
10. A long insulated copper wire is closely wound as a spiral of $N$ turns. The spiral has inner radius $a$ and outer radius $b$. The spiral lies in the $X-Y$ plane and a steady current $I$ flows through the wire. The $Z$-component of the magnetic field at the centre of the spiral is
(2011)
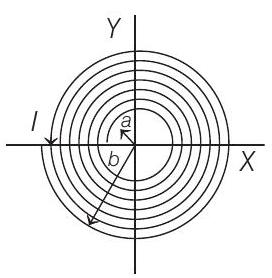
(a) $\frac{\mu _0 N I}{2(b-a)} \ln \frac{b}{a}$
(b) $\frac{\mu _0 N I}{2(b-a)} \ln \frac{b+a}{b-a}$
(c) $\frac{\mu _0 N I}{2 b} \ln \frac{b}{a}$
(d) $\frac{\mu _0 N I}{2 b} \ln \frac{b+a}{b-a}$
Show Answer
Answer:
Correct Answer: 10. (a)
Solution:
- If we take a small strip of $d r$ at distance $r$ from centre, then number of turns in this strip would be,
$$ d N=\frac{N}{b-a} d r $$
Magnetic field due to this element at the centre of the coil will be
$$ \begin{aligned} \quad d B & =\frac{\mu _0(d N) I}{2 r}=\frac{\mu _0 N I}{(b-a)} \frac{d r}{r} \\ \therefore \quad B & =\int _{r=a}^{r=b} d B=\frac{\mu _0 N I}{2(b-a)} \ln \frac{b}{a} \end{aligned} $$






