Magnetics 2 Question 10
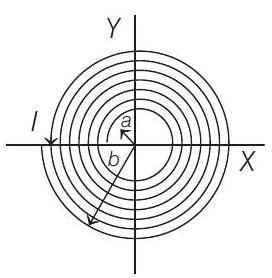
10. A long insulated copper wire is closely wound as a spiral of
(2011)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 10. (a)
Solution:
- If we take a small strip of
Magnetic field due to this element at the centre of the coil will be






