Laws of Motion 5 Question 9
9. A smooth semicircular wire track of radius $R$ is fixed in a vertical plane (figure). One end of a massless spring of natural length $3 R / 4$ is attached to the lowest point $O$ of the wire track. A small ring of mass $m$ which can slide on the track is attached to the other end of the spring. The ring is held stationary at point $P$ such that the spring makes an angle $60^{\circ}$ with the vertical. The spring constant $k=m g / R$. Consider the instant when the ring is making an angle $60^{\circ}$ with the vertical. The spring is released, (a) Draw the free body diagram of the ring. (b) Determine the tangential acceleration of the ring and the normal reaction.
$(1996,5 M)$
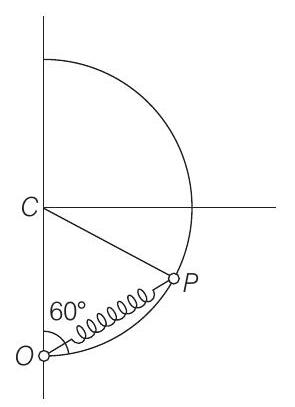
Show Answer
Solution:
- $C P=C O$
Radius of circle $(R)$
$\therefore \angle C P O=\angle P O C=60^{\circ}$
$\therefore \angle O C P$ is also $60^{\circ}$.
Therefore, $\triangle O C P$ is an
equilateral triangle.
Hence, $O P=R$
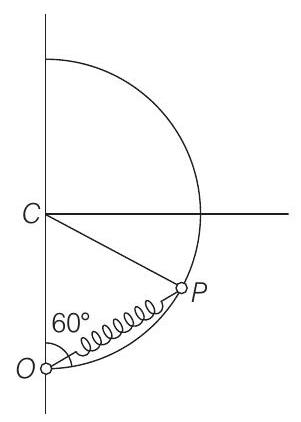
Natural length of spring is $3 R / 4$.
$\therefore$ Extension in the spring
$\Rightarrow$ Spring force,
$$ x=R-\frac{3 R}{4}=\frac{R}{4} $$
$$ F=k x=\frac{m g}{R} \quad \frac{R}{4}=\frac{m g}{4} $$
The free body diagram of the ring will be as shown below.
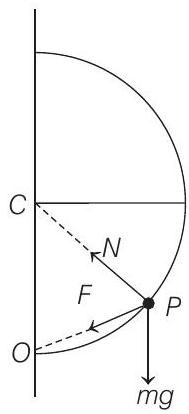
Here, $F=k x=\frac{m g}{4}$ and $N=$ Normal reaction.
(b) Tangential acceleration, $\boldsymbol{a}_{\boldsymbol{T}}$ The ring will move towards the $x$-axis just after the release. So, net force along $x$-axis
$$ \begin{aligned} F_{x} & =F \sin 60^{\circ}+m g \sin 60^{\circ} \\ & =\frac{m g}{4} \frac{\sqrt{3}}{2}+m g \frac{\sqrt{3}}{2} \\ F_{x} & =\frac{5 \sqrt{3}}{8} m g \end{aligned} $$
The free body diagram of the ring is shown below.
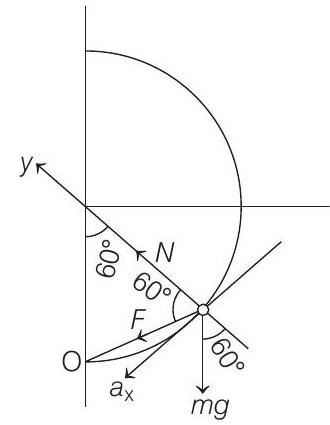
Therefore, tangential acceleration of the ring,
$$ a_{T}=a_{x}=\frac{F_{x}}{m}=\frac{5 \sqrt{3}}{8} g \Rightarrow a_{T}=\frac{5 \sqrt{3}}{8} g $$
Normal reaction, $N$ Net force along $y$-axis on the ring just after the release will be zero.
$$ \begin{aligned} & F_{y}=0 \\ \therefore \quad & N+F \cos 60^{\circ}=m g \cos 60^{\circ} \\ \therefore \quad & =m g \cos 60^{\circ}-F \cos 60^{\circ} \\ & =\frac{m g}{2}-\frac{m g}{4} \frac{1}{2}=\frac{m g}{2}-\frac{m g}{8} \\ & N=\frac{3 m g}{8} \end{aligned} $$






