SATHEE: Laws of Motion 5 Question 9

Laws of Motion 5 Question 9

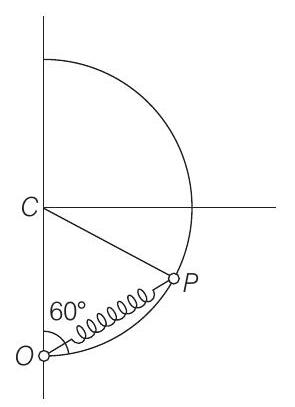
9. A smooth semicircular wire track of radius $R$ is fixed in a vertical plane (figure). One end of a massless spring of natural length $3 R / 4$ is attached to the lowest point $O$ of the wire track. A small ring of mass $m$ which can slide on the track is attached to the other end of the spring. The ring is held stationary at point $P$ such that the spring makes an angle $60^{\circ}$ with the vertical. The spring constant $k = m g / R$ . Consider the instant when the ring is making an angle $60^{\circ}$ with the vertical.

The spring is released, (a) Draw the free body diagram of the ring. (b) Determine the tangential acceleration of the ring and the normal reaction.

$(1996, 5$ M)

Show Answer

Solution:

$C P = C O$

Radius of circle $(R)$

$∴ ∠ C P O = ∠ P O C = 60^{\circ}$

$∴ ∠ O C P$ is also $60^{\circ}$ .

Therefore, $△ O C P$ is an

equilateral triangle.

Hence, $O P = R$

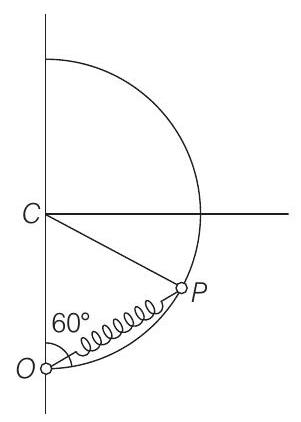
Natural length of spring is $3 R / 4$ .

$∴$ Extension in the spring

$\Rightarrow$ Spring force,

$x = R - \frac{3 R}{4} = \frac{R}{4}$

$F = k x = \frac{m g}{R} \frac{R}{4} = \frac{m g}{4}$

The free body diagram of the ring will be as shown below.

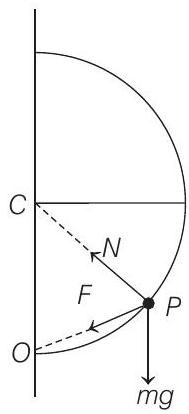
Here, $F = k x = \frac{m g}{4}$ and $N =$ Normal reaction.

(b) Tangential acceleration, $a_{T}$ The ring will move towards the $x$ -axis just after the release. So, net force along $x$ -axis

$\begin{aligned} F_{x} & = F \sin 60^{\circ} + m g \sin 60^{\circ} \\ = \frac{m g}{4} \frac{\sqrt{3}}{2} + m g \frac{\sqrt{3}}{2} \\ F_{x} & = \frac{5 \sqrt{3}}{8} m g \end{aligned}$

The free body diagram of the ring is shown below.

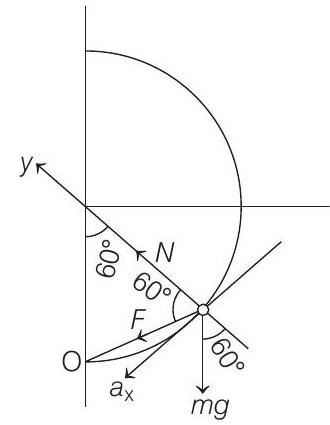
Therefore, tangential acceleration of the ring,

$a_{T} = a_{x} = \frac{F_{x}}{m} = \frac{5 \sqrt{3}}{8} g \Rightarrow a_{T} = \frac{5 \sqrt{3}}{8} g$

Normal reaction, $N$ Net force along $y$ -axis on the ring just after the release will be zero.

$\begin{aligned} F_{y} = 0 \\ ∴ & N + F \cos 60^{\circ} = m g \cos 60^{\circ} \\ ∴ & = m g \cos 60^{\circ} - F \cos 60^{\circ} \\ = \frac{m g}{2} - \frac{m g}{4} \frac{1}{2} = \frac{m g}{2} - \frac{m g}{8} \\ N = \frac{3 m g}{8} \end{aligned}$