Laws of Motion 4 Question 7
7. A simple pendulum of length
(1986, 2M)
(a)
(b)
(c) The magnitude of the tangential acceleration of the bob
(d)
Show Answer
Answer:
Correct Answer: 7. (b, c)
Solution:
- Motion of pendulum is the part of a circular motion. In circular motion, it is better to resolve the forces in two perpendicular directions. First along radius (towards centre) and second along tangential. Along radius, net force should be equal to
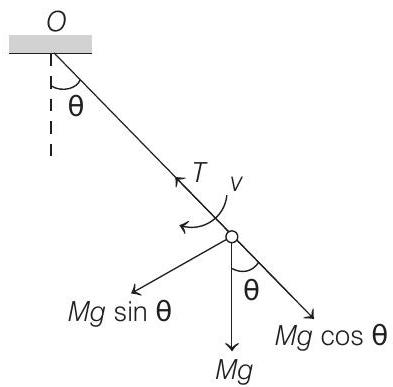
and






