Laws of Motion 4 Question 7
7. A simple pendulum of length $L$ and mass (bob) $M$ is oscillating in a plane about a vertical line between angular limits $-\varphi$ and $+\varphi$. For an angular displacement $\theta(|\theta|<\varphi)$, the tension in the string and the velocity of the bob are $T$ and $v$ respectively. The following relations hold good under the above conditions.
(1986, 2M)
(a) $T \cos \theta=M g$
(b) $T-M g \cos \theta=\frac{M v^{2}}{L}$
(c) The magnitude of the tangential acceleration of the bob $\left|a _T\right|=g \sin \theta$
(d) $T=M g \cos \theta$
True/False
Show Answer
Answer:
Correct Answer: 7. (b, c)
Solution:
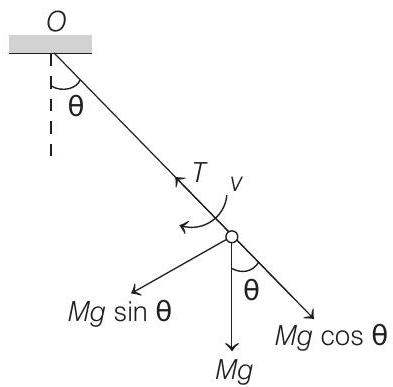
- Motion of pendulum is the part of a circular motion. In circular motion, it is better to resolve the forces in two perpendicular directions. First along radius (towards centre) and second along tangential. Along radius, net force should be equal to $\frac{m v^{2}}{R}$ and along tangent it should be equal to $m a _T$, where $a _T$ is the tangential acceleration in the figure.
$$ T-M g \cos \theta=\frac{M v^{2}}{L} $$
and
$$ M g \sin \theta=M a _T \text { or } a _T=g \sin \theta $$
