Laws of Motion 4 Question 10
10. A hemispherical bowl of radius $R=0.1 \mathrm{~m}$ is rotating about its own axis (which is vertical) with an angular velocity $\omega$. A particle of mass $10^{-2} \mathrm{~kg}$ on the frictionless inner surface of the bowl is also rotating with the same $\omega$. The particle is at a height $h$ from the bottom of the bowl.
(a) Obtain the relation between $h$ and $\omega$. What is the minimum value of $\omega$ needed, in order to have a non-zero value of $h$ ?
(b) It is desired to measure $g$ (acceleration due to gravity) using the set-up by measuring $h$ accurately. Assuming that $R$ and $\omega$ are known precisely and that the least count in the measurement of $h$ is $10^{-4} \mathrm{~m}$, what is minimum possible error $\Delta g$ in the measured value of $g$ ?
$(1993,3+2 M)$
Show Answer
Answer:
Correct Answer: 10. (a) $h=R-\frac{g}{\omega^{2}}, \omega_{\min }=\sqrt{\frac{g}{R}}=9.89 \mathrm{rad} / \mathrm{s}$
(b) $9.8 \times 10^{-3} \mathrm{~m} / \mathrm{s}^{2}$
Solution:
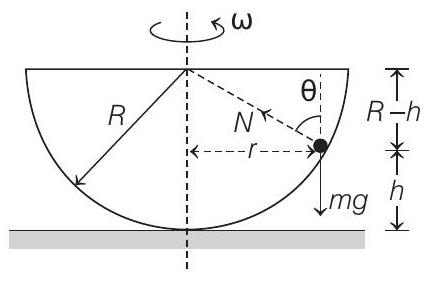
Given, $R=0.1 \mathrm{~m}, m=10^{-2} \mathrm{~kg}$
(a) FBD of particle in ground frame of reference is shown in figure. Hence,
and $\quad N \sin \theta=m r \omega^{2}$
Dividing Eq. (ii) by Eq. (i), we obtain
$$ \begin{aligned} \tan \theta & =\frac{r \omega^{2}}{g} \text { or } \frac{r}{R-h}=\frac{r \omega^{2}}{g} \\ \text { or } \quad \omega^{2} & =\frac{g}{R-h} \end{aligned} $$
This is the desired relation between $\omega$ and $h$. From Eq. (iii),
$$ h=R-\frac{g}{\omega^{2}} $$
For non-zero value of $h$,
$$ R>\frac{g}{\omega^{2}} \text { or } \omega>\sqrt{g / R} $$
Therefore, minimum value of $\omega$ should be
or
$$ \begin{aligned} \omega_{\min } & =\sqrt{\frac{g}{R}}=\sqrt{\frac{9.8}{0.1}} \mathrm{rad} / \mathrm{s} \\ \omega_{\min } & =9.89 \mathrm{rad} / \mathrm{s} \end{aligned} $$
(b) Eq. (iii) can be written as $h=R-\frac{g}{\omega^{2}}$
If $R$ and $\omega$ are known precisely, then $\Delta h=-\frac{\Delta g}{\omega^{2}}$
or $\Delta g=\omega^{2} \Delta h$ (neglecting the negative sign)
$$ (\Delta g)_ {\min }=\left(\omega_ {\min }\right)^{2} \Delta h,(\Delta g)_{\min }=9.8 \times 10^{-3} \mathrm{~m} / \mathrm{s}^{2} $$






